3.2 Reconnaissance de mots enchaînés

La base TIDIGIT contient aussi des « phrases » qui sont des suites de chiffres^3.2. Les mêmes locuteurs ont produit les mots isolés et les phrases.

Nous allons présenter la modification effectuée sur l’algorithme précédent pour reconnaître des phrases à partir des modèles créés avec des mots isolés. Cependant les résultats obtenus sont décevants du fait de l’absence de prise en compte des effets de coarticulation. En effet, ces derniers introduisent des modifications acoustiques importantes aux frontières des mots adjacents. Ensuite, nous montrerons comment nous avons segmenté les phrases de l’espace d’apprentissage pour obtenir des mots en contexte. En effet, ceux-ci permettent généralement d’obtenir de meilleurs scores de reconnaissance puisqu’ils permettent de prendre en compte la variabilité due à la coarticulation. Or la base utilisée n’a pas été segmentée préalablement. Enfin nous présenterons les contraintes supplémentaires imposées aux transitions entre deux modèles dans le but de mieux prendre en compte cette variabilité. Pour conclure, nous comparerons les avantages et les points faibles respectifs des modèles de Markov et de la méthode présentée dans ce chapitre.

3.2.1 Modification de l’algorithme de reconnaissance

Nous modifions l’algorithme présenté page 

qui effectue la reconnaissance de mots en ajoutant un « niveau phrase ». En effet, reconnaître une phrase implique la comparaison d’une locution à l’ensemble des concaténations de mots possibles, pour cela il faut :

– déterminer le nombre de mots de la phrase,
– reconnaître chacun des mots. Ces deux tâches peuvent être conduites simultanément comme l’ont fait remarquer Bridle et Nakagawa [1], [2]. Les modifications à apporter à l’algorithme sont :

– les modifications des contraintes de manière à ce que le chemin optimal puisse être composé d’une concaténation de mots,
– la mémorisation à chaque instant du mot précédemment reconnu afin de retrouver la suite de mots prononcée.

3.2.1.0.1 Nouvel algorithme

Le niveau phrase introduit des contraintes sur les transitions entre les différents modèles. Dans la base utilisée (choisie pour permettre une comparaison des résultats obtenus en reconnaissance de mots isolés avec d’autres travaux utilisant des modèles de Markov) toutes les transitions entre différents modèles sont possibles car il n’y a pas de contrainte syntaxique.

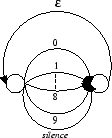
Figure 3.7 : Modèle des séquences de chiffres

Le nouvel algorithme est semblable à celui qui permet de reconnaître les mots isolés. Seulement le taux de dissemblance à l’état 0 au temps t de chaque automate
n’est plus initialisé à l’infini, mais en respectant les contraintes du niveau phrase :

(3.1)

où est un état final de et parcourt l’ensemble des automates. La figure 3.7 illustre le « langage » reconnu correspondant à cette nouvelle contrainte : toutes les séquences de chiffres sont possibles, le symbole représentant le mot vide. Le long des transitions étiquetées par les chiffres ou le silence, le calcul se conduit comme précédemment.

Par ailleurs, à chaque instant et pour tout les états finaux des automates, nous mémorisons le modèle précédemment reconnu, ce qui permet de retrouver la suite de mots prononcée. La figure 3.8 illustre le principe du décodage (backtracking) de la suite reconnue. Le dernier état final du chemin optimal (Pred) ainsi que l’instant où il a été atteint (Temps) sont mémorisés à chaque étape afin qu’il soit possible de retrouver la suite de mots effectivement prononcée. Ainsi, à la fin de la deuxième locution (3), le meilleur état final du troisième modèle () référence l’état final du modèle au temps correspondant à la fin de la locution précédente(1).

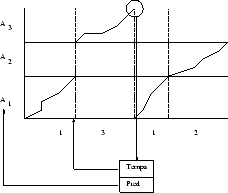
Figure 3.8 : Principe de la reconnaissance de mots enchaînés

3.2.2 Nouvel apprentissage

Les locutions de TIDIGIT sont entourées de silence. Ceci n’est pas gênant pour la reconnaissance de mots isolés. En effet, dans ce cas le silence du modèle sera mis en correspondance avec celui de la locution à reconnaître. Cependant, les chiffres qui constituent les « phrases » ne sont pas tous séparés par du silence. Il faut donc le supprimer lors de la construction du modèle. Pour cela nous utilisons deux critères : le nombre de passages par zéro du signal ainsi que son énergie. Avec le silence ainsi extrait nous construisons un automate. Le vocabulaire est maintenant constitué des 11 chiffres et du silence.

3.2.3 Evaluation du taux de reconnaissance

Maintenant, l’évaluation du taux de reconnaissance doit tenir compte des substitutions, mais aussi des insertions et des omissions de mots. Toutefois le silence est supprimé des phrases reconnues avant comparaison puisqu’il n’est pas transcrit dans le corpus. Ensuite, on définit deux taux de reconnaissance :

– le taux de mots reconnus,
– le taux de phrases reconnues, c’est-à-dire dans lesquelles il n’y a ni insertion, ni omission, ni substitution de chiffre.

Les tableaux 3.3, 3.4 et 3.5 illustrent la comparaison de deux chaînes. La première et la deuxième chaîne, respectivement en abscisse et en ordonnée, sont représentées en gras. Ces séquences de symboles sont comparées en utilisant la distance suivante :
si
, . Les tableaux représentent le cumul des coûts le long des chemins optimaux (tableau 3.4), la longueur de ces chemins (tableau 3.3) et finalement le chemin optimal (tableau 3.5). En fixant le coût local d’une substitution (ou confusion) de symbole à , le nombre de substitutions entre les deux chaînes est égal à la somme des coûts le long du chemin optimal. Le nombre d’insertions de symboles dans la première chaîne par rapport à la deuxième correspond au nombre de transitions horizontales et le nombre d’omissions de symboles au nombre de transitions verticales dans ce chemin. Sur l’exemple, il y a donc une substitution (un 1 au lieu d’un 3) et une insertion (un 3). Le nombre de mots reconnus est égal à la longueur de la phrase du modèle moins le nombre de substitutions. Ici cela donne mots reconnus.

3.2.3.1 Premiers résultats

Les premiers résultats ont donné de l’ordre de 60% de phrases reconnues. Ce faible score peut s’expliquer puisque les mots en contexte subissent de fortes modifications dues aux effets de coarticulation. Afin de prendre en compte cet effet, nous devons ajouter dans les automates des locutions extraites de phrases. Pour cela il nous faut segmenter celles-ci, c’est-à-dire déterminer le début et la fin de chacun des mots à l’intérieur d’une phrase. La partie suivante décrit la démarche.

3.2.4 Segmentation

Pour segmenter une phrase, on modifie légèrement l’algorithme de reconnaissance de manière à contraindre le système à reconnaître la suite de chiffres prononcée par le locuteur. Nous commençons par créer une instance de modèle pour chaque chiffre de la phrase. Entre chacun des chiffres, ainsi qu’en début et fin de phrase, il peut y avoir du silence.

Figure 3.9 : Contraintes pour la segmentation

La figure 3.9 illustre les contraintes imposées à la reconnaissance pour segmenter le mot « 9279 ». La modification de l’algorithme se traduit donc par les mêmes contraintes que précédemment (cf. équation 3.1) où est maintenant une instance soit de silence, soit du modèle du mot précédent et où parcourt ses états finaux. Le décodage permet alors de retrouver les début et fin des différents mots prononcés.

3.2.5 Problèmes rencontrés lors de la segmentation

L’algorithme de segmentation automatique ne nous a pas donné satisfaction puisqu’il a conduit à des mots de durée irréaliste : 4 échantillons soit 64ms pour certains. Nous avons donc modifié les contraintes à l’intérieur des modèles de mots afin de remédier à ce problème :

– suppression des boucles dans les automates,
– utilisation des contraintes de Sakoe et Shiba symétriques ; avec celles-ci, les dilatations temporelles ne peuvent varier que dans l’intervalle
. La segmentation a alors donné des résultats beaucoup plus réalistes. Cependant, il est à noter que l’évaluation de la qualité d’une segmentation est un problème difficile. On peut citer, par exemple, les travaux du CSLU  [3] dans lesquels diverses segmentations de phrases en phonèmes faites par des experts de langues maternelles différentes sont comparées. Or il n’y avait pas d’accord parfait entre les experts, que ce soit à propos des étiquettes ou bien encore des frontières entre les phonèmes.

3.2.6 Résultats

Nous avons conservé les contraintes de Sakoe et Chiba symétriques lors de la reconnaissance. L’amélioration est significative : désormais le taux de reconnaissance s’élève à 93,3% pour les phrases entièrement correctes tandis que le taux de mots reconnu est de 97,7%.

Le tableau 3.6 présente les substitutions, le tableau 3.7 les insertions ; tandis que les omissions sont consignées dans le tableau 3.8.

Cependant, ils ne sont pas encore à la hauteur de ceux obtenus par Bocchieri et Wilpon [4]. En utilisant des modèles de Markov à 10 états comprenant 64 mixtures de vecteurs cepstraux, ils obtiennent en effet sur TIDIGIT des taux de reconnaissance supérieurs à selon les caractéristiques de la paramétrisation cepstrale et atteignant même .

3.2.7 Prise en compte du contexte droit

Comme l’effet de coarticulation dépend évidemment du couple de mots adjacents, nous avons introduit des contraintes de manière à n’autoriser les transitions entre un état final d’un automate et l’état initial de l’automate
seulement lorsque la locution dont est issue la branche se terminant en était suivie d’une prononciation dont le modèle est .

Pour cela il faut mémoriser le contexte droit des prononciations qui forment l’automate. La modification apportée à l’algorithme devient :

où est un état final de ayant pour contexte droit.

3.2.7.1 Résultats

Nous n’avons pas noté d’amélioration des résultats obtenus. Deux raisons peuvent expliquer cet échec. D’une part la quantification vectorielle ne prend pas en compte le contexte : la seule information temporelle utilisée est la dérivée des vecteurs et les transitions ne sont pas bien modélisées par la quantification vectorielle qui recherche au contraire des prototypes dans les zones denses. En second lieu, le nombre de locutions utilisées pour construire un modèle avec prise en compte du contexte est 12 fois plus grand que précédemment. Il est impossible pour des raisons d’espace mémoire de stocker autant de références, or un nombre insuffisant de locutions de référence conduit à une chute du taux de reconnaissance (cf. section 3.1.3).

3.2.8 Conclusion

Dans cette partie, nous avons présenté une méthode de reconnaissance de mots qui s’inspire des premiers travaux en RAP (Reconnaissance Automatique de Parole) mais qui a donné des résultats comparables à ceux obtenus en utilisant des modèles de Markov lors de la résolution du problème de la reconnaissance de mots isolés. Elle conduit cependant à des taux de reconnaissance plus faibles lorsqu’il s’agit de la reconnaissance de phrases. Il est maintenant intéressant de comparer les deux méthodes, pour d’une part apprécier leurs avantages respectifs et d’autre part mieux cerner les points faibles communs.

Les modèles de Markov utilisent une topologie fixée a priori, tandis que leurs probabilités de transition entre états ainsi que les densités d’observation à l’intérieur des états sont sujettes à un ajustement statistique. Au contraire, dans la méthode décrite ci-dessus, les observations sont quantifiées au départ tandis que l’apprentissage se réduit à ajouter des locutions codées dans le graphe. En utilisant des HMM, on admet l’hypothèse de l’indépendance Markovienne :
« la probabilité d’observer o à l’état q au temps t dépend de l’état où l’on se trouvait au temps t-1 ». Or cette hypothèse est vraiment mauvaise dans le cas de la parole réelle. Le nombre d’états est généralement petit et de ce fait, il suffit de relativement peu de prononciations pour entraîner correctement un modèle simple. On dispose de plusieurs choix pour effectuer l’estimation initiale des paramètres. L’estimation au maximum de vraisemblance conduit à l’amélioration du modèle pour chaque mot. L’inconvénient de cette démarche est de ne pas prendre en compte l’ensemble du lexique à reconnaître. Par conséquent, pour avoir des modèles plus discriminants, on estime les paramètres avec l’algorithme de MMIE ou Corrective Training (cf. page 

). La réestimation des paramètres peut se faire de manière bayésienne.

La démarche décrite dans cette partie ne requiert pas l’hypothèse markovienne. Cependant, le nombre d’états est grand, c’est pourquoi il a été utile de quantifier les locutions. En outre, la quantification vectorielle projette les locutions dans le domaine quéfrentiel et l’on perd ainsi de l’information temporelle. Ceci peut partiellement expliquer les résultats relativement mauvais obtenus en reconnaissance de mots enchaînés et l’échec de la prise en compte du contexte. En effet, les zones les plus affectées par la coarticulation sont les extrémités des mots. Les vecteurs acoustiques des extrémités ne sont pas bien représentés par les classes issues de la quantification vectorielle.

Les difficultés rencontrées lors de la reconnaissance de mots enchaînés sont la détermination du nombre de mots et la reconnaissance correcte malgré la coarticulation. Le premier problème est élégamment résolu avec l’algorithme de Viterbi pour les HMM, et par la programmation dynamique à deux niveaux dans la méthode décrite dans cette partie. Cependant la modélisation de la durée est un problème dans les HMM. En effet, sans modèle explicite de la longueur des observations, la probabilité de rester dans un état décroît exponentiellement—à cause de la probabilité de transition inférieure à 1—avec le temps ce qui n’est pas réaliste. La méthode décrite ci-dessus règle ce problème grâce à l’alignement temporel des séquences. Pour pallier l’effet de coarticulation, on peut utiliser plusieurs modèles par entrée lexicale ou utiliser des mixtures de gaussiennes dans le cas de modèles semi-continus. Ceci conduit à une augmentation du nombre de paramètres et nécessite donc un grand corpus d’apprentissage pour que l’estimation soit bonne. Avec les automates, la prise en compte du contexte échoue dans la prise en compte de la coarticulation.

Une autre difficulté est due au changement d’environnement. En effet, les taux de reconnaissance chutent lorsque le locuteur est mal représenté dans l’espace d’apprentissage ou que le bruit ambiant, le microphone...est différent lors de la reconnaissance. Le fait de représenter assez explicitement chaque locution permet aux automates de s’adapter rapidement comme l’a montré l’expérience réalisée en mots isolés. La faiblesse des HMM, qui pallient le manque de représentativité de l’espace d’apprentissage en ré-estimant de manière bayésienne les paramètres, est le « mélange » à l’intérieur d’une même observation du bruit inhérent à la mesure du signal et des informations concernant le locuteur, l’environnement... lorsqu’on ne dispose pas de modèles paramétriques pour cela.

Le chapitre suivant présente une démarche qui s’est répandue ces dernières années et qui a pour ambition de modéliser la production de la parole, afin de pouvoir extraire du signal acoustique les gestes des différents articulateurs.