Résumé–Sommaire

3.1 Reconnaissance de mots isolés

3.1.1 Introduction

Les modèles de Markov (Hidden Markov Models, HMM) nécessitent un apprentissage long—ce qui en soit n’est pas un problème—mais demandent aussi un corpus représentatif pour chaque mot à reconnaître, ce qui n’est pas sans poser quelques difficultés. En outre, la topologie du modèle de Markov est fixée a priori et n’est pas modifiée lors de l’apprentissage. En effet, seules les probabilités de transition entre les différents états et les probabilités d’observation à l’intérieur de ces derniers sont ajustées à l’aide des algorithmes classiques d’apprentissage dans les modèles de Markov. Le choix de la topologie initiale est donc un problème délicat. Des tentatives ont vu le jour pour introduire des connaissances phonétiques ou/et phonologiques lors de la construction de la topologie du modèle [1], [2].

La méthode que nous proposons est inspirée des premiers travaux en reconnaissance automatique de la parole, à l’époque où l’on utilisait un taux de dissemblance entre la locution à reconnaître et des locutions de référence, calculé grâce à la programmation dynamique. Les travaux ont pour origine la thèse de Joseph Di Martino [3] qui a utilisé les travaux de Sakoe et Chiba [4]. Cependant les coûts de cette technique sont élevés que ce soit en mémoire, pour sauvegarder les locutions de référence, ou en temps CPU à la reconnaissance. Par ailleurs l’article de Baum-Welch [5] à donné une preuve de convergence de l’algorithme du MLE (Maximum Likelihood Estimation) qui fut dès lors utilisé dans les modèles de Markov. Ceci a contribué au déclin de l’approche par programmation dynamique. Cependant en construisant un dictionnaire de vecteurs acoustiques (avec l’algorithme de quantification de Linde Buzo et Gray LBG [6]) puis en codant les locutions de référence tout en les factorisant à gauche, nous avons pu réduire l’espace mémoire et le temps de calcul requis ce qui permet d’obtenir de très bons résultats en reconnaissance de mots isolés comme nous allons le voir dans les sections suivantes.

3.1.2 Apprentissage

La base de donnée utilisée est TIDIGIT qui a servi à de nombreuses études. Le choix de cette base permet de comparer les résultats obtenus avec d’autres travaux. Le signal est échantillonné à $f_{e}=$ 20kHz. La parole n’est pas bruitée. Le vocabulaire est formé des 11 chiffres anglo-saxons (o et zero pour le 0). Pour l’apprentissage, nous disposons de 55 locuteurs, des hommes adultes de divers états des USA. Chacun d’eux a prononcé deux fois l’ensemble des chiffres, ce qui fait 110 locutions de référence par mot. L’apprentissage s’effectue suivant les étapes suivantes :

– paramétrisation du signal,
– construction du dictionnaire,
– construction de l’automate. Nous allons détailler ces trois étapes.

3.1.2.1 Paramétrisation du signal

Nous utilisons l’analyse cepstrale (cf. section 2.2.3) pour analyser le signal. Cette analyse suppose l’hypothèse couramment admise : le signal de parole résulte de la convolution de sources (vibrations des cordes vocales, bruit de friction) avec la fonction de transfert du conduit vocal.

Tous les 256 échantillons (16ms) nous extrayons du signal acoustique préaccentué

$s(i)=x(i)-0.96x(i-1)$

des fenêtres de $N=512$ échantillons ce qui correspond à une durée de 32ms—une puissance de deux étant idéale pour la FFT (Fast Fourier Transform)— Le fenêtrage utilisé est celui de Hamming

$h(i)=0.54-0.46\cos \left( \frac{2\pi i}{N-1}\right) ,\, i\in [0,N-1]$

et
$h(i)=0,\, i\geq N$ . La transformée de Fourier à court terme de ,

$\widetilde{s}_{\tau }(f)=\sum _{i=-\infty }^{\tau }s(i)h(\tau -i)e^{-\frac{2\pi fi}{N}}$

est calculée pour compris entre 0 et la fréquence de Nyquist
$\frac{f_{e}}{2}=$ 10kHz. Puis nous calculons le logarithme
$\log _{\cal C}\left( \widetilde{s}_{\tau }\right)$ défini par
$\log _{\cal C}(z)=\log (\left\vert z\right\vert )+j\arg (z)$ où $z\in \cal C$ . Enfin nous intégrons ce logarithme suivant 20 canaux répartis selon une échelle fréquentielle non linéaire mel :

$1\, mel=1125\log (0.0016f+1)\, Hz$

où est la fréquence en Hz et la fréquence en mel. Cette échelle a l’ambition de modéliser la sensibilité de l’oreille humaine. Une transformée de Fourier inverse fournit les coefficients. Les premiers d’entre eux, qui contiennent le plus d’information au sujet de la fonction de transfert du conduit vocal, sont conservés 23.

Ainsi nous obtenons un vecteur de paramètres MFCC (Mel Frequency scaled Cepstral Coefficient)
$\overrightarrow{c}$ toutes les 16ms. L’étape suivante consiste à quantifier cet espace i.e. à trouver l’ensemble de prototypes
$\overrightarrow{p}_{k}$ le plus représentatif de cet ensemble de vecteurs.

3.1.2.2 Construction du dictionnaire

Nous utilisons l’algorithme LBG (Linde Buzo Gray 56). La construction est itérative : le premier prototype
$\overrightarrow{p}_{1}$ est le centre de gravité de l’ensemble des vecteurs cepstraux, la première partition est constituée d’une seule partie. Puis nous divisons chaque partie en deux, itérativement, jusqu’à l’obtention du nombre de classes voulu.

–

$\overrightarrow{p}_{1}$

$i=1$

–

$\overrightarrow{p}_{i}$

$\overrightarrow{p}_{2i}=1.0001\overrightarrow{p}_{i}$

$d=\infty$

–

$E_{i}=\left\{ \overrightarrow{p}\left\vert \left\Vert \overrightarrow{p}-\ove... ...rrow{p}-\overrightarrow{p}_{j}\right\Vert \right. ,\forall \, j\neq i\right\}$

$i\in [1,N]$

–

$d’=\sum ^{N}_{i=0}\sum _{\overrightarrow{p}\in E_{i}}\left\Vert \overrightarrow{p}-\overrightarrow{p}_{i}\right\Vert ^{2}$

$\overrightarrow{p’}_{i}=\sum _{k\epsilon E_{i}}\overrightarrow{p}_{k}$

–

$d’<d$

$p_{i}$

$p_{i}’$

$d’$

–

À l’aide des codebooks obtenus, nous codons les locutions en remplaçant chaque vecteur par l’indice du prototype le plus proche. Nous obtenons ainsi un ensemble de suites de vecteurs prototypes comme modèle pour chacun des mots. Par exemple, sur la figure 3.1, l’ensemble des vecteurs cepstraux est partitionné en 4 classes. La locution représentée par la flèche—qui donne le sens du temps— sera codée 4, 3, 2, 2, 2, 2, 1, 1, 1, 4, 1.

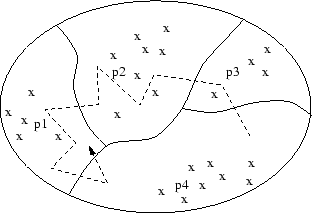
**Figure 3.1 :** Construction d’un dictionnaire et codage d’une locution.
Construction d’un dictionnaire et codage d’une locution

3.1.2.3 Construction de l’automate

Pour chaque mot, nous construisons un automate en factorisant à gauche les locutions codées [7]. Cependant, afin de réduire au maximum la place mémoire nécessaire—et par conséquent le temps CPU requis pour reconnaître une locution—nous introduisons des boucles quand 4 prototypes identiques sont consécutifs. Ceci permet aussi de contraindre l’alignement temporel de telle sorte que les zones les plus stables du signal soient les plus sujettes aux dilatations et aux contractions. La figure 3.2 illustre la construction d’un tel automate. Elle représente le codage de deux locutions d’un mot et l’automate correspondant. On remarque que le premier prototype
$\overrightarrow{p}_{1}$ est factorisé. Deux boucles ont été introduites dans les parties stables du signal : pour le prototype
$\overrightarrow{p}_{3}$ dans la première locution et pour
$\overrightarrow{p}_{1}$ dans la seconde.

**Figure 3.2 :** En haut deux locutions, en bas l’automate correspondant.
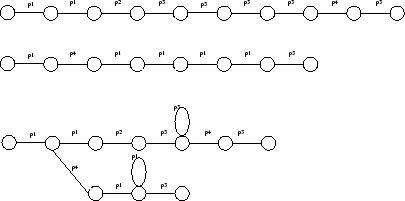
En haut deux locutions, en bas l’automate correspondant

3.1.3 Reconnaissance

Dans la base TIDIGIT, nous disposons d’un ensemble de 56 locuteurs disjoint de celui qui a servi à l’apprentissage. Ces locuteurs ont prononcé deux fois chaque mot ce qui fait
$56\times 2\times 11=1232$ mots isolés à reconnaître. Comme pour l’apprentissage, ces locutions sont paramétrisées en utilisant les MFCC. Puis elles sont codées suivant les prototypes de chacun des modèles. Enfin pour chaque locution, nous comparons son codage à l’automate du mot correspondant en utilisant la programmation dynamique.

Nous allons commencer cette section par la description du principe utilisé, puis nous décrirons les résultats obtenus :

– comparaison du taux de reconnaissance avec des résultats obtenus en utilisant un modèle de Markov discret, et incrémentalité de l’apprentissage,
– influence de la dérivée des vecteurs cepstraux, quantification des références et reconnaissance temps réel. Enfin, avant de décrire l’extension de la méthode au problème de la reconnaissance de mots enchaînés, nous discuterons ces résultats.

3.1.3.1 Principe de la reconnaissance

Nous mesurons un taux de dissemblance entre la locution à reconnaître et chacun des automates. Le mot reconnu est celui dont le modèle donne le plus petit taux de dissemblance^3.1. Celui-ci est défini comme étant le minimum des taux de dissemblance entre la locution à reconnaître et chacune des branches de l’automate. Le taux de dissemblance entre une locution paramétrisée
$\overrightarrow{c}_{i}$ ,
$i=1,\ldots,N$ et une suite de prototypes
$\overrightarrow{p}_{j}$ , $j=1,\ldots,M$ est défini par :

$D(\overrightarrow{c},\overrightarrow{p})=\min _{W}(\sum ^{K}_{k=1}\frac{d(\overrightarrow{c}_{W_{i}(k)},\overrightarrow{p}_{W_{j}(k)})P(W(k-1),W(k))}{N(W)})$

où
$W=(W_{i},W_{j})$ est un chemin de recalage, c’est-à-dire une fonction de $[1,\ldots,K]$ dans
$[1,\ldots,N]\times [1,\ldots,M]$ croissante au sens large (pour rendre compte de l’écoulement du temps) et telle que $W(1)=(1,1)$ et $W(K)=(N,M)$ . $d(.,.)$ est une distance dans l’espace des vecteurs cepstraux, nous avons utilisé une distance euclidienne.
est une pondération qui dépend de contraintes locales imposées à et

$N(W)=\sum ^{K}_{k=1}P(W(k-1),W(k))$

est un facteur de normalisation rendant
$D(\overrightarrow{c},\overrightarrow{p})$ indépendant de la longueur du chemin.

Ces chemins de recalage permettent de tenir compte des différents débits d’élocution en comparant des locutions de longueurs différentes de manière judicieuse. En effet le changement du débit d’élocution n’affecte pas également tout les phonèmes et par conséquent le recalage linéaire
$W_{i}=\frac{N}{M}W_{j}$ ne suffit pas. La figure 3.3 donne un exemple de recalage temporel.

**Figure 3.3 :** Recalage temporel.
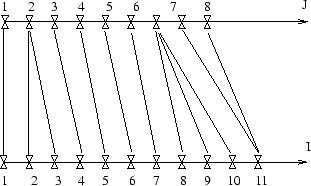
Recalage temporel

Mais le calcul des taux de dissemblance pour chacun des chemins est excessivement coûteux. En effet, il existe $M^{N}$ chemins satisfaisant ces contraintes. Heureusement, la programmation dynamique permet le calcul du chemin optimal
(qui minimise
$D(\overrightarrow{c},\overrightarrow{p})$ ) avec un coût en ${\cal O}(N.M)$ opérations.

Soit un chemin optimal qui conduit de $(i_{1},j_{1})$ à $(i_{2},j_{2})$ . Alors si $(i,j)\in W$ , le chemin menant de $(i_{1},j_{1})$ à est lui aussi optimal.

Maintenant, des contraintes assurent que chaque vecteur de la locution à reconnaître est mis en correspondance avec un prototype. Posons $W_{o}(i,j)$ le chemin optimal entre et . Alors ce chemin est composé d’un chemin optimal
$W_{o}(i-1,j_{0})$ et d’un chemin entre $(i-1,j_{0})$ et . On peut donc calculer pour chaque tous les chemins optimaux tels que $W_{i}=i$ . La recherche du chemin optimal est donc en
${\cal O}(N.M)$ . En outre, il suffit maintenant de mémoriser $2N$ taux de dissemblance car les coûts des chemins arrivant en $(i-2,j)$ ne sont pas utilisés pour calculer les coûts de ceux qui aboutissent en .

La figure 3.4 présente trois exemples de contraintes locales, ainsi que les pondérations . Deux types de pondérations sont habituellement choisis :

– les pondérations symétriques :
$P(W(k-1),W(k))=W_{i}(k)-W_{i}(k-1)+W_{j}(k)-W_{j}(k-1)$ donc
$N(W)=W_{i}+W_{j}$
– les pondérations asymétriques :
$P(W(k-1),W(k))=W_{i}(k)-W_{i}(k-1)$ donc
$N(W)=W_{i}$

**Figure 3.4 :** Contraintes locales : asymétrique, symétrique, de Sakoe et Chiba symétrique.
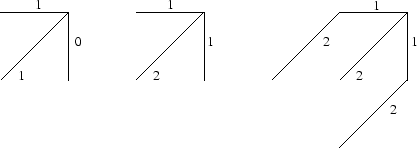
Contraintes locales : asymétrique, symétrique, de Sakoe et Chiba symétrique

Nous avons choisi des contraintes qui obligent les dilatations à s’effectuer dans les zones stables (où l’on a introduit des boucles). La figure 3.5 illustre un chemin optimal possible satisfaisant ces contraintes.

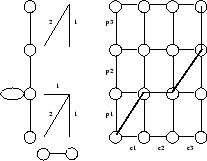
**Figure 3.5 :** Les contraintes utilisées et un exemple de chemin.
Les contraintes utilisées et un exemple de chemin

Voici l’algorithme de calcul du taux de dissemblance entre une locution et un automate :

Initialiser $C_{00}$ le cumul des distances le long du chemin optimal finissant à l’état j=0 de l’automate au temps i= 0 à 0

Pour i de 1à N
Initialiser la $C_{i0}$ à l’infini : contraindre le chemin optimal à débuter en (0,0)

Pour j de 1 au nombre d’états de l’automate
Calculer $C_{ij}=\min (\min _{j’}C_{i-1,j’}+P((i-1,j’),(i,j))*d(c_{i},p_{j}),\min _{j’\neq j}C_{ij’}+P((i,j’),(i,j))*d(c_{i},p_{j}))$ le cumul des distances le long du chemin optimal finissant en où $j’$ est un état prédécesseur de

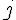
Calculer $L_{ij}$ la longueur de ce chemin en fonction des états prédécesseur de

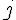
Le taux de dissemblance vaut
$\min _{j’}(\frac{C_{N,j’}}{L_{Nj’}})$ où
$j’$ est un état final de l’automate.

La figure 3.6 illustre cet algorithme.

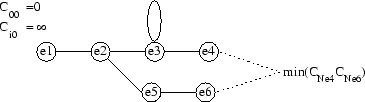
**Figure 3.6 :** Principe de la reconnaissance de mots isolés
Principe de la reconnaissance de mots isolés

Enfin, le mot reconnu est celui dont le modèle donne le taux de dissemblance le plus petit.

3.1.3.2 Incrémentalité de l’apprentissage

Une des difficultés rencontrées lors de l’utilisation des modèles de Markov est la réestimation des paramètres (moyenne et matrice de covariance à l’intérieur des états pour les modèles semi-continus et probabilités de transition). En effet, étant donnée la manière dont s’effectue l’apprentissage, les locuteurs mal représentés dans le corpus, ou les conditions différentes (milieux bruités, microphones différents lors de l’acquisition du corpus d’apprentissage et de la reconnaissance...) font chuter le pourcentage de mots reconnus. Nous avons donc testé la possibilité pour notre système d’apprendre à corriger ses erreurs. Pour cela, les locutions mal reconnues sont codées puis ajoutées dans le modèle correspondant.

En utilisant 23 coefficients cepstraux et 256 prototypes, nous avons obtenu un taux de reconnaissance de 98.5% soit 19 erreurs sur 1232 locutions à reconnaître. Ces résultats sont comparables aux 99.4% obtenus en utilisant des modèles de Markov discrets [8]. Après adjonction de ces 19 locutions dans les automates correspondants, seules 4 erreurs subsistaient, soit un taux de reconnaissance de 99.9%.

3.1.3.3 Reconnaissance temps réel

À chaque instant, notre algorithme effectue autant de calculs de distance qu’il y a de vecteurs prototypes, et autant de comparaisons qu’il y a d’états dans les automates. Le nombre de prototypes étant fixé, le coût croît de façon linéaire en fonction du nombre d’états.

Pour réduire la place mémoire ainsi que le temps CPU nécessaires à la reconnaissance d’un mot, nous devons diminuer le nombre d’états, par exemple en choisissant un sous-ensemble des locutions de la base d’apprentissage comme locutions de référence. Pour cela nous avons développé un algorithme de quantification des formes de référence. D’autre part, certains auteurs ont remarqué que l’utilisation de la dérivée des coefficients cepstraux améliorait les taux de reconnaissance. Ceci est à rapprocher de l’utilisation de modèles de Markov d’ordre 2 ou des modèles de trajectoire de Gong [9]. L’amélioration des performances s’explique par l’apport d’information sur l’évolution des paramètres. Dans un premier temps nous allons présenter l’influence de la dérivée des paramètres puis nous décrirons l’algorithme de quantification des formes de référence.

3.1.3.4 Influence de la dérivée des coefficients cepstraux

Comme l’ont remarqué certains auteurs [10], la prise en compte d’informations sur la cinétique des paramètres améliore souvent les taux de reconnaissance. Nous avons donc utilisé la dérivée des coefficients cepstraux. Une pondération $p_{1}=0,48$ a été calculée pour donner la même influence aux vecteurs cepstraux qu’à leur dérivée. La distance entre deux paramètres pour lesquels les vecteurs cepstraux sont respectivement
$\overrightarrow{u}$ et
$\overrightarrow{v}$ , est
$\sqrt{d^{2}(\overrightarrow{u},\overrightarrow{v})+p_{1}d^{2}(\overrightarrow{u}^{’},\overrightarrow{v}^{’})}$ . Cette distance est utilisée pour quantifier le nouvel espace et pour comparer les locutions aux références.

Le tableau 3.1 donne les taux d’erreur obtenus en fonction du nombre de paramètres prototypiques retenus. En outre, nous avons utilisé seulement onze coefficients cepstraux.

Tableau 3.1 : Influence de la dérivée du vecteur cepstral

Nombre de classes	16	32	64
Taux d’erreur avec vecteurs cepstraux seuls	1.14	0.97	0.81
Taux d’erreur avec dérivée des vecteurs cepstraux	0.49	0.41	0.49

3.1.3.5 Quantification des formes de référence

L’idée de cet algorithme est de choisir seulement certaines locutions dans l’espace d’apprentissage. Cela permet d’améliorer le temps de réponse du logiciel puisque le nombre de calculs de distance est réduit. Pour cela on cherche les points correspondant au diamètre maximum de l’espace des locutions, puis on choisit parmi les deux extrémités celle qui possède la plus proche locution voisine. On cherche un deuxième point de cette manière. Puis nous divisons l’espace en deux comme pour quantifier les vecteurs acoustiques. L’itération est similaire à celle de l’algorithme de quantification vectorielle.

Algorithme :

Soit l’ensemble des locutions de l’espace d’apprentissage.

–

$\overrightarrow{p}_{1}=\arg \min _{\overrightarrow{u}\in E}\max _{\overrightarrow{v}\in E}D(\overrightarrow{u},\overrightarrow{v})$

$E_{N}=E$

–

$\overrightarrow{p}_{N+1}$

$E_{N}\setminus \{\overrightarrow{p}_{N}\}$

$d=\infty$

–

$E_{i}$

$\overrightarrow{p}$

$D($

$\overrightarrow{p},\overrightarrow{p}_{i})\leq D(\overrightarrow{p},\overrightarrow{p}_{j})$

$i,j\leq N$

$j\neq i$

–

Dans l’expérience réalisée nous utilisons 22 coefficients (vecteurs cepstraux et leurs dérivées), et 32 prototypes issus de la quantification vectorielle. Le tableau suivant synthétise les résultats obtenus en fonction du nombre de formes de référence retenues.

Tableau 3.2 : Influence du nombre de références retenu

Nombre de formes	4	8	12	16	32
Taux d’erreur (%)	12.42	6.25	1.94	0.81	0.41
Temps CPU (ms)	394	496	605	709	1125

Les tests ont été effectués sur un HP 9000/755. Nous constatons que le taux de reconnaissance croît avec le nombre de prototypes utilisés. Sachant que les locutions ont une durée de l’ordre de la seconde, nous pouvons effectuer la reconnaissance en temps réel avec 16 prototypes.

3.1.4 Conclusion

La méthode décrite ci-dessus a donné des résultats comparables à ceux obtenus en utilisant des modèles de Markov discrets. En outre, elle a l’avantage de ne pas nécessiter un corpus important pour l’apprentissage. Un second point fort de cette technique est la possibilité d’effectuer un apprentissage incrémental dans le sens où une locution mal reconnue peut facilement être insérée dans l’automate. Il serait ainsi possible d’envisager une adaptation au locuteur par exemple, mais pour cela il faudrait élaguer l’automate car la borne supérieure du nombre d’états est gigantesque.

Dans la partie suivante, nous allons décrire les modifications apportées à l’algorithme pour l’adapter à la reconnaissance de mots enchaînés.

Notes

[1] L. Deng and D. X. Sun.

A statistical approach to automatic speech recognition using the
atomic speech units contructed from overlapping articulatory features.

J. Acoust. Soc. Am, 95(5):2702-2719, May 1994.

[2] H. Strik.

Using articulatory knowledge in automatic speech recognition.

In Newsletter of the Center for Language Studies (CLS)
, pages 8-13.

[3] J. Di Martino.

Contribution à la reconnaissance globale de la parole : Mots isolés
et mots enchaînés.

Thèse de 3ème cycle, 1984.

[4] H. Sakoe and S. Chiba.

A dynamic programming approach to continuous speech recognition.

In Proc. IEEE Int. Conf. Acoust., Speech, Signal Processing,
Budapest, Hungary, 1971.

[5] L.E. Baum, T. Petrie, G. Soules, and N. Weiss.

A maximization technique occurring in the statistical analysis of
probabilistic functions of markov models.

In The Annals of Mathematical Statistics, volume 41, pages
164-171, 1970.

[6] Y. Linde, A. Buzo, and R. M. Gray.

An algorithm for the vector quantizer design.

IEEE. Trans. on Communication, com. 28(1), January 1980.

[7] J. di Martino, J.-F. Mari, B. Mathieu, K. Perot K., and K. Smaïli.

Which model for future speech recognition systems : Hidden markov
models or finite-state automata.

In Proceedings of the International Conference on Acoustics,
Speech and Signal Processing, volume 1, pages 633-635, Adelaïde, Australia,
April 1994.

[8] L. R. Rabiner and S. E. Levinson.

Isolated and connected word recognition theory and selected
applications.

IEEE Trans. on Communication, 29(5):621-659, 1981.

[9] M. Afify, Y. Gong, and J.-P. Haton.

Estimation of Mixtures of Stochastic Dynamic Trajectories :
Application to Continuous Speech Recognition.

Computer, Speech and Language, 1995.

[10] E.L. Bocchieri and J.G. Wilpon.

Disciminative feature selection for speech recognition.

Computer Speech and Language, 7:229-246, 1993.