2.2 Traitements acoustiques
Les différents traitements effectués sur le signal de parole ont pour but :
– d’en donner une représentation plus concise, en conservant les informations les plus pertinentes vis-à-vis de la tâche à accomplir. Les traitements sont différents dans le cas du codage, de l’étude de la prosodie, d’une application de commande vocale ou de dictée automatique,
– d’extraire des indices permettant de segmenter la parole et de classifier les segments acoustiques obtenus. Nous verrons dans cette section les traitements les plus répandus : transformée de Fourier, analyse par prédiction linéaire, analyse cepstrale.
2.2.1 Transformée de Fourier
Tout d’abord, la figure 2.1 représente une vue d’un signal de parole. La figure 2.2 en représente un segment à une échelle plus fine. Le signal présente une certaine périodicité et stationnarité à court terme. D’où l’idée de le représenter dans le domaine fréquentiel.

|
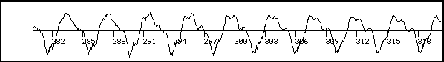
|
La transformée de Fourier d’un signal  est définie par
est définie par ]=\int _{\Re }s(t)e^{-j\omega t}{\,\rm d}t F(\omega )=[\Im (s)](\omega )]=\int _{\Re }s(t)e^{-j\omega t}{\,\rm d}t](sites/bruno/local/cache-TeX/e90e69364eb160ba13b0698bd6f1d506.png?1663819685)
où ![]() est la pulsation complexe. Cependant, comme les sons ont une durée limitée, il importe plus de connaître le spectre à court terme, c’est-à-dire les caractéristiques spectrales de la parole à un instant donné qui doivent permettre d’identifier les différents sons produits au cours du temps. En outre, il est impossible de connaître le signal de parole entre
est la pulsation complexe. Cependant, comme les sons ont une durée limitée, il importe plus de connaître le spectre à court terme, c’est-à-dire les caractéristiques spectrales de la parole à un instant donné qui doivent permettre d’identifier les différents sons produits au cours du temps. En outre, il est impossible de connaître le signal de parole entre ![]() et
et
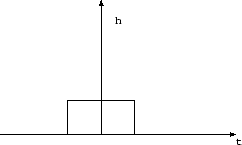
![]() (serait-ce intégrable ?). Enfin, on ne peut considérer la parole comme étant un signal périodique stationnaire que sur une durée de quelques millisecondes. C’est pourquoi on a défini la transformée de Fourier à court terme du signal comme l’analyse d’une portion de signal vue au travers d’une fenêtre temporelle h(t) comme celle représentée par la figure 2.3 :
(serait-ce intégrable ?). Enfin, on ne peut considérer la parole comme étant un signal périodique stationnaire que sur une durée de quelques millisecondes. C’est pourquoi on a défini la transformée de Fourier à court terme du signal comme l’analyse d’une portion de signal vue au travers d’une fenêtre temporelle h(t) comme celle représentée par la figure 2.3 :

|
Le prélèvement d’une partie du signal par une fenêtre induit donc une imprécision sur la valeur exacte de la transformée de Fourier du signal à une fréquence donnée. Ceci conduit à deux types de spectrogramme :
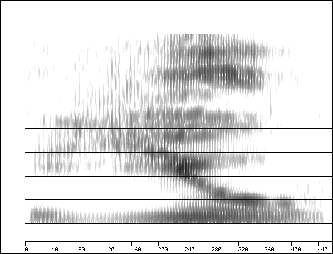
– le spectre bande large. Dans ce cas peu de points sont prélevés du signal, par conséquent la convolution intègre la « vraie » valeur du spectre sur des bandes de fréquence larges (cf. figure 2.4),
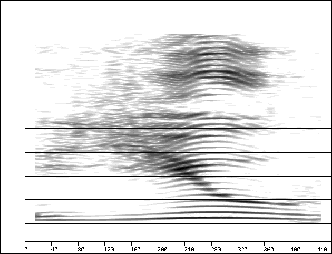
– le spectre bande étroite. Plus de points sont prélevés, le spectre de la fenêtre s’approche de la distribution de Dirac, donc la bande spectrale est de plus en plus fine (cf. figure 2.5).
|
|
En outre le signal est échantillonné et on ne le connaît qu’en certains points multiples de la période d’échantillonnage. Soit donc  le peigne de Dirac pour la fréquence
le peigne de Dirac pour la fréquence ![]() ,
, 
est le signal échantillonné. La transformée de Fourier d’un produit étant égale au produit de convolution des facteurs, on a  . Par conséquent les valeurs des transformées de Fourier de
. Par conséquent les valeurs des transformées de Fourier de ![]() et de $ s_e sont égales au facteur
et de $ s_e sont égales au facteur![]() près pour les valeurs de
près pour les valeurs de ![]() multiples de
multiples de ![]() . L’échantillonnage induit donc une périodicité de la transformée de Fourier.
. L’échantillonnage induit donc une périodicité de la transformée de Fourier.
Ces deux représentations sont complémentaires. En effet, le spectre à bande large possède une meilleure définition temporelle et permet d’identifier les fréquences de résonance du conduit vocal (larges bandes foncées) plus précisément que sur le spectre à bande étroite. Cependant celui-ci, grâce à sa meilleure définition fréquentielle, fait apparaître les harmoniques (fines bandes foncées). Il est donc plus utile pour étudier l’influence de la source glottale.
2.2.2 Analyse par prédiction linéaire
Cette technique est fort utilisée dans le codage de parole. Pour la reconnaissance de la parole, elle se justifie en considérant le modèle de parole simplifié source/conduit. Dans ce modèle, le signal de parole ![]() vaut
vaut  . La transformée en
. La transformée en ![]() conduit à
conduit à  . La fonction de transfert du conduit est donc égale à
. La fonction de transfert du conduit est donc égale à

L’analyse par prédiction linéaire conduit à estimer les coefficients de la fonction de transfert du conduit vocal. Elle estime l’échantillon courant 
en fonction des ![]() échantillons précédents :
échantillons précédents :

Soit 
l’erreur commise en estimant  par
par  . Le but est de trouver les coefficients
. Le but est de trouver les coefficients  minimisant
minimisant  .
.
En dérivant l’erreur de prédiction ![]() par rapport aux
par rapport aux  on obtient
on obtient  . Après réorganisation des termes, et en posant
. Après réorganisation des termes, et en posant  , on obtient les équations de Yule-Walker :
, on obtient les équations de Yule-Walker :

Pour résoudre ces équations, on prend une fenêtre dans laquelle ![]() varie. Ensuite deux manières permettent de construire les
varie. Ensuite deux manières permettent de construire les  :
:
– Soit on n’utilise que des  à l’intérieur de la fenêtre en fixant
à l’intérieur de la fenêtre en fixant
 en dehors. On obtient alors le calcul par la méthode d’autocorrélation. Dans ce cas, les coefficients d’autocorrélation
en dehors. On obtient alors le calcul par la méthode d’autocorrélation. Dans ce cas, les coefficients d’autocorrélation  peuvent être obtenus soit directement à partir du signal temporel, soit comme transformée de Fourier inverse du spectre de puissance obtenu, par exemple, à partir d’une simulation dans le domaine fréquentiel. La résolution des équations de Yule-Walker s’effectue en utilisant l’algorithme de Durbin [1].
peuvent être obtenus soit directement à partir du signal temporel, soit comme transformée de Fourier inverse du spectre de puissance obtenu, par exemple, à partir d’une simulation dans le domaine fréquentiel. La résolution des équations de Yule-Walker s’effectue en utilisant l’algorithme de Durbin [1].
– Soit on conserve les vraies valeurs de  à l’extérieur de la fenêtre où
à l’extérieur de la fenêtre où ![]() varie, et on résout le système par la méthode de covariance. Pour cela il faut inverser la matrice symétrique des
varie, et on résout le système par la méthode de covariance. Pour cela il faut inverser la matrice symétrique des  . À partir des coefficients ainsi calculés, il est possible de rechercher les racines du dénominateur de l’équation 2.1 qui correspondent aux modes de résonance du conduit vocal (formants). Or les trois premières fréquences de résonance sont suffisantes pour caractériser les voyelles du français. Cette analyse est donc utilisée pour paramétrer le signal acoustique afin d’alimenter une architecture de reconnaissance, mais aussi pour l’estimation précise des valeurs des fréquences des formants.
. À partir des coefficients ainsi calculés, il est possible de rechercher les racines du dénominateur de l’équation 2.1 qui correspondent aux modes de résonance du conduit vocal (formants). Or les trois premières fréquences de résonance sont suffisantes pour caractériser les voyelles du français. Cette analyse est donc utilisée pour paramétrer le signal acoustique afin d’alimenter une architecture de reconnaissance, mais aussi pour l’estimation précise des valeurs des fréquences des formants.
2.2.3 Analyse par transformée homomorphique
Cette méthode a pour but de séparer les contributions du conduit vocal et des sources. D’après le modèle source/conduit, la parole est le résultat d’une convolution de la source par le filtre constitué du conduit vocal et de la radiation aux lèvres :  . Le but est de déconvoluer ce produit de convolution de manière à séparer les contributions respectives de la source et du conduit.
. Le but est de déconvoluer ce produit de convolution de manière à séparer les contributions respectives de la source et du conduit.
Pour cela on utilise la propriété de la transformée de Fourier : la transformée de Fourier d’un produit de convolution est égale au produit des transformées de Fourier des facteurs. Puis on utilise la propriété du logarithme : le logarithme d’un produit est égal à la somme des logarithmes facteurs. On retourne dans un domaine pseudo-temporel par une transformée de Fourier inverse, la transformée de Fourier inverse d’une somme étant égale à la somme des transformées de Fourier inverse des termes, il résulte alors de ces transformations une contribution additive de la source et du conduit. La fonction obtenue est appelée cepstre et le domaine dans laquelle elle prend ses valeurs est appelé domaine quéfrentiel. Pour les sons voisés, le cepstre présente un pic à une distance égale à la période fondamentale  . En revanche, la contribution de la source est localisée principalement dans les premiers coefficients du cepstre. On peut alors appliquer un filtre pour séparer les premiers coefficients des derniers : on appelle ce filtrage liftrage. La réponse impulsionnelle du conduit vocal peut s’obtenir en appliquant un filtre qui supprime les derniers coefficients, puis en appliquant successivement une transformée de Fourier, une exponentiation et une transformée de Fourier inverse. Les coefficients cepstraux calculés sur une échelle Mel ou Bark peuvent servir directement à alimenter une architecture de reconnaissance de la parole.
. En revanche, la contribution de la source est localisée principalement dans les premiers coefficients du cepstre. On peut alors appliquer un filtre pour séparer les premiers coefficients des derniers : on appelle ce filtrage liftrage. La réponse impulsionnelle du conduit vocal peut s’obtenir en appliquant un filtre qui supprime les derniers coefficients, puis en appliquant successivement une transformée de Fourier, une exponentiation et une transformée de Fourier inverse. Les coefficients cepstraux calculés sur une échelle Mel ou Bark peuvent servir directement à alimenter une architecture de reconnaissance de la parole.
2.2.4 Analyses dérivées de LPC
Des considérations sur la perception conduisent à des variantes des analyses purement mathématiques précédentes. Par exemple, l’analyse par prédiction linéaire perceptivement fondée est basée sur l’analyse par prédiction linéaire dans laquelle on utilise des critères psychoacoustiques afin d’obtenir un spectre auditif [2], [3].
L’analyse RASTA-PLP a pour but d’améliorer la robustesse du système de reconnaissance en milieu bruité. Elle est basée sur l’analyse PLP [4], [5].
2.2.5 Conclusion
Différentes méthodes permettent d’analyser le signal acoustique. Cette analyse est différente selon l’architecture de reconnaissance qu’elle alimente. Pour les systèmes à base de connaissances, on essaie d’extraire du signal acoustique les indices qu’utilisent les experts humains pour classifier les sons. Pour les architectures stochastiques, neuromimétiques basées sur le principe de la comparaison dynamique de formes acoustiques, on cherche une représentation du signal acoustique pertinente (c’est-à-dire qui conserve les caractéristiques discriminantes entres les différents sons) et concise (de manière à pouvoir effectuer les calculs en temps réel).
Nous allons maintenant présenter les architectures les plus couramment utilisées en reconnaissance automatique de la parole.
Notes
[1] L. R. Rabiner and R. W. Schafer.
Digital Processing of Speech.
Prentice-Hall, Englewood Cliffs, N.J., 1978.
[2] H. Hermansky, B.A. Hanson, and H. Wakita.
Low-dimensional representation of vowels based on all-pole modeling
in the psychophysical domain.
In Speech communication, volume 4, pages 181-187, 1985.
[3] Y. Anglade.
Robustesse de la reconnaissance automatique de la parole :
étude et application dans un système d’aide vocal pour une standardiste
mal-voyante.
PhD thesis, CRIN&INRIA, Nancy, France, 1994.
[4] H. Hermansky, N. Morgan, A. Bayya, and P. Kohn.
Compensation effect of the communication channel in auditory-like
analysis of speech.
In Eurospeech, pages 1367-1370, September 1991.
[5] Y. Anglade.
Robustesse de la reconnaissance automatique de la parole :
étude et application dans un système d’aide vocal pour une standardiste
mal-voyante.
PhD thesis, CRIN&INRIA, Nancy, France, 1994.