2.3 Architectures pour la reconnaissance

Cette section présentera brièvement les différentes architectures utilisées en reconnaissance de parole, depuis les débuts lorsque l’on comparait des formes acoustiques de référence à la parole à reconnaître en utilisant un algorithme de recalage temporel pour pallier les distorsions dues en particulier au débit d’élocution, jusqu’aux réseaux neuromimétiques réputés excellents pour leur pouvoir de discrimination, en passant par les systèmes à base de connaissances qui ont abouti à une meilleure compréhension de la production et de la perception de la parole et aux modèles de Markov qui donnent actuellement les meilleurs taux de reconnaissance.

2.3.1 La comparaison de formes

Il s’agit de comparer la parole à des formes acoustiques de référence. Cette technique a surtout été utilisée pour des applications de reconnaissance monolocuteur de mots. La principale source de variabilité dans ce contexte est constituée par les distorsions dues aux différences dans les débits d’élocution. Cette difficulté a été résolue en utilisant l’algorithme de recalage temporel (Dynamic Time Warping).

Le problème du recalage temporel est résolu en utilisant le principe de programmation dynamique. Ce principe permet de trouver le meilleur chemin dans un réseau. Pour l’appliquer à la reconnaissance de parole, les noeuds du graphe sont obtenus en faisant le produit cartésien du modèle et de la forme acoustique à reconnaître comme l’illustre la figure 2.6.

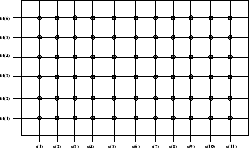
Figure 2.6 : Réseau

Les arcs sont orientés pour prendre en compte l’écoulement du temps. Un coût est associé aux transitions. Le meilleur chemin est celui de coût le plus faible. En construisant réseaux, pour autant de modèles, on obtient chemins dont un de plus faible coût. La forme acoustique reconnue est celle qui correspond à la projection de ce chemin sur l’axe des ordonnées.

Pour reconnaître des mots enchaînés, on considère toutes les concaténations possibles des modèles. Cette méthode a été utilisée dans la première expérience de cette thèse (cf.chapitre 3).

2.3.2 Les modèles à base de connaissances

Utilisés principalement pour des applications devant traiter un grand vocabulaire, lorsqu’il n’est pas envisageable de prendre le mot comme forme acoustique de référence, ces méthodes ont beaucoup apporté en terme de compréhension de la perception et de la production de la parole. Il s’agit de construire une base de connaissances à partir de l’expertise des phonéticiens et phonologues sous forme de règles [1]. Les indices acoustiques extraits du signal sont ensuite utilisés pour construire une base de faits. Les règles pour lesquelles les prémisses sont satisfaits peuvent alors êtres appliquées pour enrichir cette base. Le principe de l’extraction des connaissances est illustré par la figure 2.7.

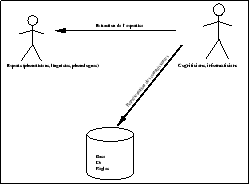
Figure 2.7 : Construction de la base de règles.

Le processus de reconnaissance est schématisé sur la figure 2.8. Le traitement du signal produit des faits acoustiques. Ceux-ci servent de prémisses aux règles modélisant l’expertise humaine. L’application de ces règles produit de nouveaux faits qui enrichissent à leur tour la base. Ainsi à partir d’indices acoustiques (existence d’une barre d’explosion ayant telles propriétés, suivie par un noyau vocalique...) des faits de niveau supérieur (phonétiques, phonologiques, linguistiques) sont produits.

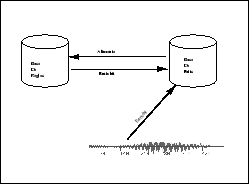
Figure 2.8 : Principe de la reconnaissance avec un système à base de connaissances.

La difficulté majeure dans cette approche consiste à construire la base de règles. En effet les experts ne sont généralement pas unanimement d’accord. Par ailleurs, l’adjonction de nouvelles connaissances doit préserver la cohérence de la base, ce qui n’est pas toujours aisé à vérifier. En outre, les règles dépendent souvent de la langue ce qui réduit aussi la portée d’une telle architecture.

Néanmoins les aspects multidisciplinaires de cette approche sont intéressants et ont beaucoup apporté en terme de compréhension de ce qui caractérise la parole. En effet la comparaison dynamique de formes ne prend guère en compte les particularités du signal de parole, si ce n’est à travers les traitements acoustiques qui peuvent être fondés sur un modèle de production rudimentaire (modèle source/conduit).

2.3.3 Les modèles neuromimétiques

Les deux architectures précédentes ont un important point faible : l’apprentissage. Dans les systèmes basés sur la comparaison de formes acoustiques, le choix des références, la qualité de leur acquisition et les traitements appliqués conditionnent les résultats en reconnaissance. Dans le cas des systèmes à base de connaissances c’est la construction de la base de règles, avec les difficultés inhérentes à l’extraction du savoir-faire des phonéticiens, phonologues et linguistes  [2] qui constitue l’apprentissage.

Le principe original du courant neuromimétique est de modéliser le système de perception de l’humain en construisant un réseau dont les états correspondent aux « neurones » tandis que les liens sont l’équivalent des « synapses » les reliant, par analogie avec le système nerveux humain. En effet, pour les tâches de perception, l’humain est très performant et robuste comparé aux technologies numériques actuelles. C’est pourquoi les réseaux de neurones formels sont utilisés en reconnaissance de formes en général. Cependant, ils peuvent aussi être vus comme une simple classe d’algorithmes parallèles, en oubliant les fondements biologiques qui leur ont donné naissance. La diffusion de la connaissance au travers du réseau conduit à une meilleure robustesse et l’architecture est intrinsèquement parallèle ce qui facilite les implantations efficaces. En outre, des algorithmes d’apprentissage permettent, à partir d’exemples, de distribuer la connaissance automatiquement au travers du réseau ce qui simplifie grandement le développement d’applications. Ainsi l’algorithme de rétropropagation de l’erreur  [3] a suscité un regain d’intérêt pour ces architectures. Ce n’est cependant pas le seul algorithme d’apprentissage pour un réseau à couches non récurrent. Montana et Davis  [4], par exemple, utilisent un algorithme génétique.

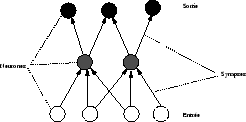
Figure 2.9 : Architecture neuronale.

La figure 2.9 illustre une architecture neuronale classique^2.1. L’apprentissage par rétropropagation consiste à présenter une entrée au réseau et à calculer la sortie correspondante. Cette sortie est comparée à la sortie attendue . La différence entre la sortie observée et celle calculée par le réseau est utilisée pour modifier les poids synaptiques :

– Phase de propagation : soit le vecteur d’entrée, l’activation d’un neurone de la couche cachée est calculée par
où sont les poids des synapses et la fonction d’activation—qui calcule la sortie du neurone caché en fonction de la combinaison linéaire des entrées. De même
permet de calculer les composantes de la couche de sortie en fonction de la couche intermédiaire.
– Phase de rétropropagation : soit maintenant les composantes du vecteur attendu en sortie. Le but est de modifier les et
afin de minimiser
où . En résolvant
on obtient la formule
et
où l’on a posé . Ainsi on voit que l’erreur en sortie permet de calculer l’erreur de la couche cachée, d’où le nom de rétropropagation de l’erreur. La connaissance est ainsi inférée à partir d’exemples. Les poids sont ajustés de manière itérative jusqu’à ce que la différence entre la sortie calculée et la sortie observée soit minime. Par exemple, en reconnaissance d’écriture, on présente en entrée une matrice de pixels, et en sortie un vecteur de dimension le nombre de lettres de l’alphabet, dont toutes les coordonnées sont nulles sauf celle correspondant à la lettre fournie en entrée qui vaut . Lors de la reconnaissance, on présente une matrice de pixels. Le neurone de sortie ayant la plus grande activation correspond à la lettre reconnue.

Deux types de réseau sont couramment utilisés en reconnaissance automatique de la parole : les réseaux récurrents (Jordan, Elman [5]) dans lesquels les sorties et/ou neurones de la couche cachée réactivent les entrées (cf. figure 2.10), ceci afin de prendre en compte l’écoulement temporel, et les réseaux à couches comme celui représenté sur la figure 2.9. Ces derniers sont généralement utilisés au sein d’autres architectures (à base de connaissances, modèles de Markov...) pour leur pouvoir de discrimination. Par exemple François  [6] utilise des perceptrons multicouches pour améliorer la discrimination entre /p/, /t/ et /k/ au sein du système APHODEX. Des algorithmes d’apprentissage par l’exemple existent pour ces différentes architectures. Pour discriminer entre /no/ et /go/, Watrous et Shastri utilisent un réseau récurrent  [7]. Wang et al.  [8] utilisent un réseau de Hopfield comme post-processeur dans un réseau de croyance bayésien pour reconnaître les chiffres en Mandarin. Haton donne encore d’autres exemples d’utilisation des réseaux neuronaux isolés et couplés à d’autres architectures dans  [9].

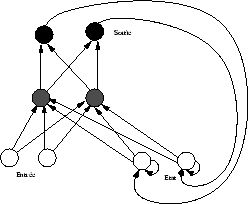
Figure 2.10 : Réseau récurrent de Jordan.

2.3.4 Les modèles de Markov

Le principe de la modélisation par des modèles de Markov discrets est le suivant : on mesure une variable aléatoire discrète et on cherche à modéliser le processus qui en est à l’origine par un modèle stochastique. Pour cela on se donne états correspondant chacun à une observation potentielle. La probabilité d’une observation est supposée ne dépendre que de la suite d’observations déjà effectuée et non pas du temps. Selon le nombre d’observations passées servant à estimer la probabilité d’une nouvelle observation, on obtient des modèles de Markov discrets de différents ordres. Pour l’ordre 1, on obtient donc
. On peut représenter le modèle par un vecteur de probabilité a priori d’être dans un état et une matrice de probabilité de transiter entre un état et un état . Un tel modèle est représenté par la figure 2.11. Entre deux états quelconques, il existe un arc qui les relie : ce type de modèle est appelé modèle ergodique.

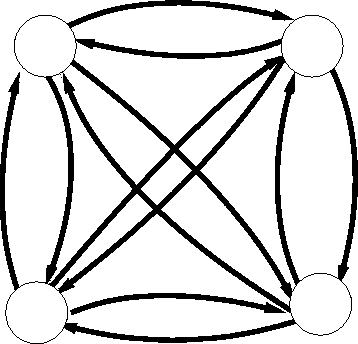
Figure 2.11 : Modèle ergodique.

Dans les modèles de Markov cachés les observations ne sont pas directement observables. À chaque état correspond une distribution de probabilité d’observations. Ainsi un modèle de Markov caché discret est représenté par :

– un vecteur de probabilité de se trouver a priori dans un état ,
– une matrice de transition entre les états et
– une distribution de probabilité des observations à l’intérieur de chaque état.

L’avantage par rapport aux modèles de Markov observables en parole est la possibilité d’utiliser un modèle gauche-droite (cf. figure 2.12), dans lequel la topologie du graphe représente naturellement l’axe du temps. Les différentes distributions de probabilité à l’intérieur des états peuvent être interprétées comme les caractéristiques acoustiques modélisées.

Une fois choisie la topologie du graphe, il faut estimer les paramètres, c’est-à-dire les coefficients de la matrice de transition, les coefficients du vecteur des probabilités initiales et les distributions de probabilité dans les états. Pour cela, un algorithme célèbre et efficace a été trouvé. Il s’agit de l’estimation de Baum-Welch, appelée aussi forward-backward algorithm. En outre, des critères de convergence existent pour cet algorithme [10].

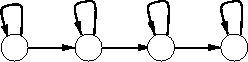
Figure 2.12 : Modèle gauche-droite.

Après avoir entraîné autant de modèles que de formes acoustiques à reconnaître, on peut calculer la probabilité d’une séquence d’observations connaissant chacun des modèles. La forme acoustique reconnue est celle dont l’état final du modèle est le plus probable.

De la même manière que lors de la comparaison de formes acoustiques (cf. section 2.3.1) on peut construire un graphe en reliant les états initiaux et finaux des différents modèles afin de reconnaître des enchaînements de formes acoustiques. La reconnaissance est alors effectuée en utilisant l’algorithme de Viterbi (principe de la programmation dynamique).

L’existence d’algorithmes d’apprentissage par des exemples et la preuve de convergence ont contribué au succès de cette approche. La modélisation stochastique est d’ailleurs aussi utilisée pour modéliser le langage  [11], ou pour d’autres tâches de perception comme la reconnaissance de l’écriture [12]. Comme pour les modèles neuromimétiques, l’apprentissage s’effectue à l’aide d’exemples et par conséquent les problèmes de modélisation de l’expertise humaine ne se posent pas immédiatement. Néanmoins plusieurs difficultés subsistent comme le choix de la topologie (nombre d’états principalement), la distribution de probabilité à l’intérieur des états (mesure discrète, mixtures de gaussiennes...) ou encore la modélisation de la durée  [13].

À ses début, la modélisation markovienne modélisait séparément chaque forme acoustique en utilisant l’algorithme d’apprentissage MLE (Maximum Likelihood Estimation). Ceci conduisait à une discrimination assez pauvre pour les formes acoustiques proches et à un regain d’intérêt pour les réseaux neuromimétiques réputés pour leur pouvoir discriminant [14]. Il existe maintenant des algorithmes qui permettent de pallier ce problème. Ainsi Bahl et al.  [15] proposent un algorithme qui maximise non plus la vraisemblance de chaque modèle, mais le taux de reconnaissance sur l’espace d’apprentissage. Il utilise pour cela deux coefficients qui visent à inhiber les probabilités des transitions qui sont à l’origine des erreurs (d’où le nom de Corrective Training), et à maximiser les autres, comme la règle de Hebb dans les réseaux neuronaux. Même s’ils ne démontrent pas la convergence de l’algorithme, ce dernier a donné expérimentalement de bons résultats. Il a été adapté pour la reconnaissance de mots enchaînés par Lee  [16], [17] dans le système SPHINX. Un autre algorithme a amélioré le pouvoir discriminant des HMM. Il s’agit de l’apprentissage MMIE (Maximum Mutual Information Estimation). Tandis que MLE maximise la probabilité a posteriori de l’espace d’apprentissage pour chaque modèle, MMIE maximise la probabilité a posteriori du modèle correspondant aux données, puisque ce critère est celui utilisé pour le décodage de la phrase. L’apprentissage des paramètres d’un modèle tient compte des autres modèles afin d’améliorer le pouvoir discriminant. Ceci conduit cependant à une beaucoup plus grande complexité de l’apprentissage. Cardin, Normandin et al. ont commencé à appliquer cet algorithme pour la reconnaissance de mots isolés  [18]. Puis ils présentent dans  [19] des approximations rendant possible l’utilisation d’un tel algorithme pour la reconnaissance de mots enchaînés. Dans  [20], ils donnent une solution possible au choix du nombre de mixtures par état dans un modèle de Markov en utilisant MMIE. En effet, une bonne modélisation nécessite assez de paramètres pour modéliser précisément les caractéristiques acoustiques de l’espace d’apprentissage, mais d’un autre côté l’estimation d’un grand nombre de paramètres requiert un immense espace d’apprentissage.