4.6 Inversion acoustique-articulatoire dans le modèle de Maeda
Cette section décrit les expériences que nous avons menées afin d’obtenir les trajectoires des paramètres du modèle de Maeda à partir des formants extraits de la parole d’un locuteur. Elle présentera successivement une description plus détaillée du modèle, puis la normalisation effectuée pour adapter ce modèle à notre locuteur. Enfin elle décrira la méthode d’inversion et les résultats obtenus.
4.6.1 Le modèle de Maeda
Comme nous utilisons ce modèle dans la suite, nous allons le présenter brièvement ici. Maeda a noté dans [1] que les deux premières composantes principales d’une analyse de tracés de contours de la langue extraits de clichés radiographiques et projetés sur une grille semi-polaire (cf. figure 4.3) permettaient d’expliquer 90% de la variance des données originales. En utilisant les 3 premières composantes principales, il a remarqué que ce taux s’élevait à 98%. Mieux, il a donné une interprétation des 3 composantes principales calculées : l’une d’elles correspond à un déplacement avant/montant et arrière/descendant de la langue, la deuxième à une contraction dans une direction arrière/montante. La troisième correspond à une compression/dilatation de la langue dans le plan sagittal plus difficilement interprétable. C’est pourquoi dans [2] il a utilisé une connaissance a priori du système articulatoire : la langue comporte 3 articulateurs (dorsal, apical et corps de la langue). Elle est fixée à la mâchoire inférieure qui est contrôlée par un articulateur. Pour utiliser cette connaissance il a utilisé le modèle général de composantes linéaires décrite dans [3]. Stone et al. [4] utilisent aussi une analyse en composantes principales pour les sections transversales de la langue. Ceci leur permet de caractériser certains traits articulatoires des voyelles. Le modèle que nous utilisons comprend en outre deux paramètres pour déterminer l’ouverture et la protrusion des lèvres, et un paramètre pour fixer la hauteur du larynx. Cependant le modèle a été construit à partir des clichés d’une locutrice précise, or les tailles du pharynx et de la bouche différent entre les hommes, les femmes et les enfants [5], [6]. Le modèle est donc muni de deux facteurs d’échelle pour contrôler leur longueur. À partir d’images de notre locuteur, nous avons déterminé ces deux coefficients.

Modèle articulatoire original sur sa grille semi-polaire
|
4.6.2 Acquisition des images et de la parole
La première étape de notre expérience consiste à adapter le modèle à notre locuteur. Cette étape a pour but de permettre au modèle de recouvrir l’espace acoustique du locuteur [7], [8]. Pour cela, nous avons utilisé des images IRM de son conduit vocal et enregistré la parole correspondante.
Acquisition des images
Nous avons utilisé une machine SIGNA de General Electic pour l’acquisition des images et retenu les mêmes paramètres que Yang [9]. Nous avons réalisé trois séries d’images pour les voyelles orales françaises /i, y, e, ,
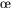
, ø, a, , , o, u/ : une série de coupes sagittales passant par le sillon de la langue et deux dans des plans parallèles à 5mm de distance. En effet, les clichés ayant servi à construire le modèle étant des images aux rayons X, elles ne laissent pas apparaître ce sillon. La série d’images en meilleure adéquation avec le modèle était la série du plan de gauche et nous l’avons retenue pour la suite.
À partir de ces images, nous avons développé un logiciel pour extraire manuellement les contours et les projeter sur la grille semi-polaire permettant de repérer les contours dans le modèle de Maeda. Nous avons ainsi extrait les vecteurs correspondant au contour de la langue, à la paroi dure, la protrusion de lèvres, leur aperture et la hauteur de larynx pour chacune des voyelles.
Enregistrement de la parole
L’inconvénient majeur de l’imagerie IRM est l’intensité du bruit émis par la machine qui interdit l’analyse de la parole produite lors de l’acquisition des images. Nous avons donc enregistré le locuteur dans le bruit, puis nous lui avons demandé de reproduire chacune des voyelles dans le silence tout en écoutant à l’aide d’un casque l’enregistrement du bruit. C’est à partir de cette parole que nous avons extrait les caractéristiques acoustiques utilisées pour l’adaptation. Celles-ci sont les valeurs des fréquences des trois premiers formants, car elles suffisent à différencier les voyelles du français (niveau de la perception) et sont affiliées à des cavités du conduit vocal [10] (niveau de la production). Ces valeurs sont extraites du signal de parole grâce à l’analyse par prédiction linéaire (cf. section 2.2.2). Pour comparer ces valeurs à celles obtenues par simulation, nous avons utilisé la même procédure pour extraire les fréquences des formants produits par le modèle bien que d’autres techniques puissent être utilisées : dérivée seconde du spectre de transfert (cf. [11]), modèle acoustique de la parole (cf. [12], chapitre 4) par exemple.
4.6.3 Adaptation des échelles et estimation du contour extérieur
Le modèle de Maeda a été construit d’après des images d’une locutrice adulte. Or chez les hommes adultes le conduit vocal est plus long que chez les femmes, et par ailleurs le rapport des tailles du pharynx et de la cavité antérieure est plus grand [13]. Notre locuteur étant un homme la première adaptation a porté sur les facteurs d’échelle pour le pharynx et pour la bouche du modèle. Pour cela, nous avons superposé le modèle et les images et modifié ces deux paramètres en se basant sur les contours extérieurs du conduit vocal (la paroi dure). Nous avons trouvé une taille du pharynx de 18% supérieure à celui du modèle, et une bouche 8% plus grande. Ces valeurs ne sont pas en désaccord avec la littérature. Ainsi Fant [14] donne un rapport typique de 11% pour la cavité buccale et 18% pour la cavité pharyngale. Ensuite le contour extérieur du modèle a été recalculé en se basant sur le contour extérieur moyen des images.
L’estimation de la qualité de l’adaptation s’effectue selon deux critères. Le premier concerne la fidélité de la modélisation : la parole synthétisée à partir des paramètres articulatoires extraits des images IRM doit correspondre à celle du locuteur. Toutefois, une erreur est tolérable puisque la parole utilisée n’est pas celle qui a effectivement été prononcée lors de l’acquisition. Le second critère a trait à la couverture de l’espace vocalique du locuteur par le modèle. Ce dernier doit être en mesure d’atteindre les voyelles prononcées par le locuteur. Les deux paragraphes suivants décrivent les résultats obtenus.
4.6.4 Fidélité du modèle
Nous avons extraits les contours des images, puis nous avons estimé les paramètres articulatoires correspondants en cherchant les paramètres qui minimisent l’erreur
 où
où ![]() est la
est la  coordonnée du contour intérieur du conduit vocal sur la grille semi-polaire, et
coordonnée du contour intérieur du conduit vocal sur la grille semi-polaire, et
 est le vecteur des sept paramètres articulatoires. Comme nous avons plus d’équations que d’inconnues, nous utilisons une décomposition en valeurs singulières afin de résoudre le système [15]. À partir de ces paramètres nous avons effectué une synthèse. Les formants obtenus sont proches de ceux produits par le locuteur.
est le vecteur des sept paramètres articulatoires. Comme nous avons plus d’équations que d’inconnues, nous utilisons une décomposition en valeurs singulières afin de résoudre le système [15]. À partir de ces paramètres nous avons effectué une synthèse. Les formants obtenus sont proches de ceux produits par le locuteur.
Les différences peuvent s’expliquer en partie par le fait que le locuteur n’a pas été capable, lors de l’enregistrement de sa parole, de reproduire fidèlement celle qu’il avait produite lors de l’acquisition des images. La table 4.1 illustre les résultats obtenus.
|
Les erreurs moyennes respectivement pour F1 F2 et F3 sont de 54Hz, 136Hz et 199Hz. Cependant on remarque que l’erreur maximale est obtenue pour chacun des formants pour une même voyelle. En fait, le locuteur ne l’a évidemment pas correctement reproduite en dépit des précautions que nous avions prises. En retirant cette voyelle, nous obtenons les erreurs moyennes suivantes : 46Hz pour F1, 111Hz pour F2, et 155Hz pour F3. On remarque que pour les voyelles d’arrière le F3 synthétique est systématiquement plus élevé que le F3 naturel, ce que notent aussi Candille et Story [16], [17].
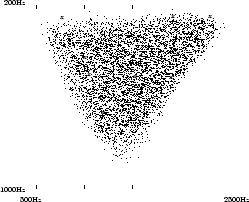
4.6.5 Couverture de l’espace vocalique du locuteur
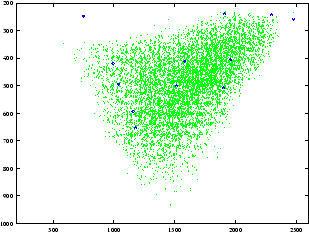
Les figures 4.4 et 4.5 représentent les projections de l’espace vocalique du locuteur respectivement dans les plans F1-F2 et F2-F3 après le calcul des deux paramètres qui contrôlent les tailles respectives du pharynx et de la bouche. Ils ont été générés en faisant varier les paramètres articulatoires autour de leur position moyenne de manière aléatoire, uniformément de ![]() à
à ![]() écarts type. Cet espace a ensuite été projeté sur les plans F1-F2 et F2-F3.
écarts type. Cet espace a ensuite été projeté sur les plans F1-F2 et F2-F3.
Espace acoustique F1-F2
|
Espace acoustique F2-F3
|
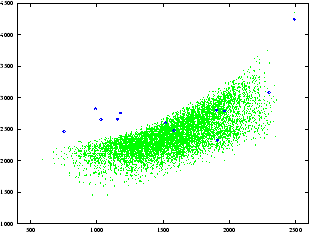
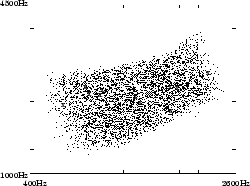
Nous avons recommencé la génération après avoir ré-estimé le contour de la paroi dure. Les figures 4.6 et 4.7 montrent les nouveaux espaces vocaliques. Une amélioration sensible de la couverture est constatée, mais certaines voyelles ne sont toujours pas atteintes.
Espace acoustique F1-F2 après ré-estimation de la paroi dure
|
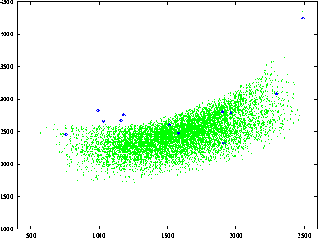
Espace acoustique F2-F3 après ré-estimation de la paroi dure
|
Plusieurs causes peuvent expliquer cette difficulté qu’a le modèle à atteindre chacune des voyelles. Une première cause de ces différences est certainement la formule de Heinz et Stevens [18] utilisée pour passer du diamètre sagittal à la fonction d’aire :
 . En effet, cette formule a été calculée sous l’hypothèse d’une langue plate à partir de cinéradiographies. Il n’y a cependant pas de consensus sur le choix d’une telle fonction [19]. Par exemple, Beautemps et al. [20] ont utilisé une formule différente lors de l’adaptation de leur modèle de coupes sagittales :
. En effet, cette formule a été calculée sous l’hypothèse d’une langue plate à partir de cinéradiographies. Il n’y a cependant pas de consensus sur le choix d’une telle fonction [19]. Par exemple, Beautemps et al. [20] ont utilisé une formule différente lors de l’adaptation de leur modèle de coupes sagittales :
 . Une autre raison peut être l’extraction du contour extérieur du conduit vocal. Les images utilisées n’étant pas de même nature que celles ayant servi à construire le modèle, nous avons obtenu un contour extérieur assez différent. Par ailleurs, ne disposant que de onze images, l’estimation du contour moyen doit aussi être entachée d’erreur. C’est pourquoi, au lieu de modifier les coefficients de la formule de Heinz, nous avons opté pour une perturbation de la forme de la paroi dure du conduit.
. Une autre raison peut être l’extraction du contour extérieur du conduit vocal. Les images utilisées n’étant pas de même nature que celles ayant servi à construire le modèle, nous avons obtenu un contour extérieur assez différent. Par ailleurs, ne disposant que de onze images, l’estimation du contour moyen doit aussi être entachée d’erreur. C’est pourquoi, au lieu de modifier les coefficients de la formule de Heinz, nous avons opté pour une perturbation de la forme de la paroi dure du conduit.
4.6.6 Adaptation de la paroi dure
Nous avons donc décidé d’optimiser itérativement le contour extérieur dans le but d’obtenir une meilleure adéquation entre la parole naturelle et celle du modèle. Pour cela, nous modifions le contour extérieur à chaque pas de l’itération d’après la fonction de sensibilité donnée par la matrice jacobienne
 où
où  est la
est la
 coordonnée sur la grille semi-polaire. Nous obtenons respectivement pour chacun des formants les erreurs résiduelles suivantes : 49Hz, 125Hz, 170Hz. Les modifications apportées à la paroi dure, à partir de la glotte et en direction des lèvres, sont résumées dans le tableau 4.2. On constate que les diminutions affectent principalement la région centrale du conduit dans la région de la luette (coefficients 10 à 13), ainsi qu’un petit peu le niveau de la glotte (premier coefficient). En revanche, la région pharyngale a dû être « élargie ». Quant à la région buccale, elle n’a pas beaucoup été affectée par cette adaptation.
coordonnée sur la grille semi-polaire. Nous obtenons respectivement pour chacun des formants les erreurs résiduelles suivantes : 49Hz, 125Hz, 170Hz. Les modifications apportées à la paroi dure, à partir de la glotte et en direction des lèvres, sont résumées dans le tableau 4.2. On constate que les diminutions affectent principalement la région centrale du conduit dans la région de la luette (coefficients 10 à 13), ainsi qu’un petit peu le niveau de la glotte (premier coefficient). En revanche, la région pharyngale a dû être « élargie ». Quant à la région buccale, elle n’a pas beaucoup été affectée par cette adaptation.
|
Bien que des écarts résiduels subsistent entre les formants du locuteur et ceux de synthèse qui correspondent aux paramètres articulatoires extraits des images IRM, l’espace acoustique du locuteur est maintenant entièrement couvert par le modèle comme le montrent les figures 4.8 et 4.9.
Espace acoustique F1-F2 finalement obtenu
|
Espace acoustique F2-F3 finalement obtenu
|
À partir du moment où le modèle parvient à reproduire la parole du locuteur, nous pouvons entreprendre l’inversion proprement dite.
4.6.7 Inversion
Les données utilisées sont des transitions entre voyelles dont les formants ont été extraits par l’algorithme de Laprie [21]. Nous n’avons pas voulu imposer une trajectoire paramétrique, ni des configurations articulatoires initiales et finales pour chaque paramètre contrairement à Candille [22] ou George [23]. Au lieu de cela un dictionnaire nous a fourni des trajectoires initiales que nous avons optimisées à l’aide d’une approche variationnelle.
Nous allons commencer par décrire la construction du dictionnaire, puis nous décrirons l’obtention des trajectoires initiales. Enfin nous présenterons la méthode variationnelle que nous utilisons pour optimiser les trajectoires ainsi obtenues.
Construction du dictionnaire
Deux méthodes ont été testées. La première consiste à faire varier les sept paramètres aléatoirement entre ![]() et
et ![]() écarts type. Ne retenant que les entrées pour lesquelles la constriction la plus faible est d’au moins
écarts type. Ne retenant que les entrées pour lesquelles la constriction la plus faible est d’au moins
 comme Boë et al. [24], nous en conservons 300000. Nous avons fait varier les paramètres au voisinage de trajectoires rectilignes entre chaque couple de configurations articulatoires obtenues (cf. page
comme Boë et al. [24], nous en conservons 300000. Nous avons fait varier les paramètres au voisinage de trajectoires rectilignes entre chaque couple de configurations articulatoires obtenues (cf. page
) pour construire le deuxième dictionnaire. De cette façon nous espérons éliminer des configurations qui ne seraient pas réalistes. Candille [25] a construit un dictionnaire semblable en choisissant des paramètres articulatoires autour de configurations articulatoires de référence associées à chaque voyelle, puis en ajoutant des points situés le long de lignes droites entre couples de configurations articulatoires de référence.
Obtention des trajectoires initiales
À partir de la parole dont nous avons extrait les formants, nous choisissons à chaque instant ![t\in [1..T] t\in [1..T]](sites/bruno/local/cache-TeX/dd20576833967f580ff69050cc5f4f46.png?1663724196) les
les ![]() meilleures entrées du dictionnaire au sens où elles produisent des formants calculés
meilleures entrées du dictionnaire au sens où elles produisent des formants calculés  proches de ceux extraits de la parole
proches de ceux extraits de la parole  . Pour cela nous utilisons une distance euclidienne entre les triplets de formants. Beautemps et Gabioud [26] utilisent une erreur basée sur les fréquences des cinq premiers formants
. Pour cela nous utilisons une distance euclidienne entre les triplets de formants. Beautemps et Gabioud [26] utilisent une erreur basée sur les fréquences des cinq premiers formants  pondérée par une estimation de leurs largeurs de bande
pondérée par une estimation de leurs largeurs de bande  mesurées :
mesurées :
 . Or d’une part il est difficile d’extraire les cinq premiers formants et d’autre part les trois premiers sont suffisants pour distinguer les voyelles du français.
. Or d’une part il est difficile d’extraire les cinq premiers formants et d’autre part les trois premiers sont suffisants pour distinguer les voyelles du français.
À partir de ces  trajectoires potentielles (cf. figures 4.10 et 4.11), nous utilisons l’algorithme de lissage de Ney [27] pour trouver la meilleure trajectoire, c’est-à-dire la plus lisse [28], [29]. En effet, un lissage linéaire ne préserve pas les discontinuités et est sensible au bruit. Dans notre cas il a pour but d’éliminer des points acoustiquement proches de la parole du locuteur, mais pour lesquels il n’y a pas de configuration articulatoire dans le dictionnaire qui permette d’obtenir une trajectoire lisse. Soit
trajectoires potentielles (cf. figures 4.10 et 4.11), nous utilisons l’algorithme de lissage de Ney [27] pour trouver la meilleure trajectoire, c’est-à-dire la plus lisse [28], [29]. En effet, un lissage linéaire ne préserve pas les discontinuités et est sensible au bruit. Dans notre cas il a pour but d’éliminer des points acoustiquement proches de la parole du locuteur, mais pour lesquels il n’y a pas de configuration articulatoire dans le dictionnaire qui permette d’obtenir une trajectoire lisse. Soit
 l’évolution des paramètres articulatoires en fonction du temps
l’évolution des paramètres articulatoires en fonction du temps ![]() . Les deux objectifs de l’algorithme sont :
. Les deux objectifs de l’algorithme sont :
– d’éliminer les instants ![]() pour lesquels il n’existe pas de
pour lesquels il n’existe pas de  permettant d’avoir une trajectoire articulatoire assez lisse,
permettant d’avoir une trajectoire articulatoire assez lisse,
– de choisir les  points
points  pour chaque instant
pour chaque instant  de manière à ce que l’évolution des paramètres articulatoires en fonction du temps
de manière à ce que l’évolution des paramètres articulatoires en fonction du temps
 soit lisse. Bien sûr, une contrainte de monotonie est imposée pour refléter l’écoulement du temps :
soit lisse. Bien sûr, une contrainte de monotonie est imposée pour refléter l’écoulement du temps :  . En outre, les conditions aux limites sont choisies telles que
. En outre, les conditions aux limites sont choisies telles que  et
et  puisque les points extrêmes peuvent ne pas être conservés. Afin d’obtenir une trajectoire lisse, on pourrait choisir comme critère à minimiser :
puisque les points extrêmes peuvent ne pas être conservés. Afin d’obtenir une trajectoire lisse, on pourrait choisir comme critère à minimiser :

où ![]() est la distance entre les paramètres articulatoires
est la distance entre les paramètres articulatoires ![]() aux temps
aux temps  et
et  . Or tous les termes de la somme sont positifs, donc ce critère ne permettrait que d’avoir une trajectoire plate voire vide ! Pour pallier cet inconvénient, un terme de bonus
. Or tous les termes de la somme sont positifs, donc ce critère ne permettrait que d’avoir une trajectoire plate voire vide ! Pour pallier cet inconvénient, un terme de bonus ![]() est retranché au coût ce qui conduit à minimiser
est retranché au coût ce qui conduit à minimiser
 . Plus
. Plus ![]() est grand, moins la courbe est lissée et plus elle contient de points. Pour l’étude de transitions entre deux voyelles, on choisit
est grand, moins la courbe est lissée et plus elle contient de points. Pour l’étude de transitions entre deux voyelles, on choisit ![]() de manière à éliminer les évolutions des paramètres articulatoires non monotones. Le problème de minimisation peut être résolu efficacement en utilisant le principe de la programmation dynamique qui consiste à introduire un coût partiel
de manière à éliminer les évolutions des paramètres articulatoires non monotones. Le problème de minimisation peut être résolu efficacement en utilisant le principe de la programmation dynamique qui consiste à introduire un coût partiel
 .
.
Cet algorithme a l’avantage de supprimer les points les plus éloignés ce qui permet de remédier dans une certaine mesure aux mauvaises entrées du dictionnaire pour lesquelles un triplet de formants proches de ceux du locuteur existe mais sans paramètre articulatoire correspondant dans le voisinage de ceux trouvés aux instants voisins. Ces trous sont ensuite comblés par interpolation linéaire, ce qui se justifie puisque les trajectoires articulatoires sont très régulières.

Ensemble de trajectoires possibles pour la position de la langue lors d’une transition /iu/ avec le premier dictionnaire
|
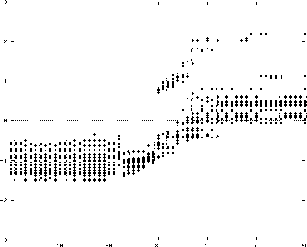
Ensemble de trajectoires possibles pour la position de la langue lors d’une transition /iu/avec le deuxième dictionnaire
|
Les trajectoires possibles en fonction du dictionnaire utilisé sont représentées par les figures 4.10 et 4.11. La figure 4.10 a été obtenue en utilisant le premier dictionnaire pour retrouver les trajectoires possibles du paramètre « position de la langue » lors d’une transition /iu/ en conservant les  meilleures configurations articulatoires. Nous remarquons que les phénomènes de compensation sont bien conservés (la dispersion des positions de la langue s’explique par la compensation due à l’ouverture de la mâchoire [30]) tandis que les trajectoires possibles sont cohérentes : /i/ est bien une voyelle avant comme l’indique la valeur négative du paramètre, tandis que /u/ est une voyelle arrière. La figure 4.11 illustre les trajectoires potentielles en utilisant le deuxième dictionnaire. Comme prévu, les configurations articulatoires ne sont pas aussi dispersées que dans le cas de l’utilisation du premier dictionnaire.
meilleures configurations articulatoires. Nous remarquons que les phénomènes de compensation sont bien conservés (la dispersion des positions de la langue s’explique par la compensation due à l’ouverture de la mâchoire [30]) tandis que les trajectoires possibles sont cohérentes : /i/ est bien une voyelle avant comme l’indique la valeur négative du paramètre, tandis que /u/ est une voyelle arrière. La figure 4.11 illustre les trajectoires potentielles en utilisant le deuxième dictionnaire. Comme prévu, les configurations articulatoires ne sont pas aussi dispersées que dans le cas de l’utilisation du premier dictionnaire.
Optimisation des trajectoires initiales
À partir des trajectoires obtenues grâce à l’inversion par tabulation et l’algorithme de Ney, nous allons itérativement améliorer la qualité de l’inversion en utilisant une approche variationnelle. En effet, les trajectoires résultant de l’inversion par tabulation et lissage ne prennent pas en compte simultanément des critères acoustiques et articulatoire. La méthode variationnelle permet de combiner de manière élégante les deux critères [31]. Le problème à résoudre est le suivant :
– obtenir une bonne qualité acoustique, c’est-à-dire minimiser
 ,
,
– obtenir une trajectoire lisse, c’est-à-dire minimiser
 ;
;
où ![]() est la pseudo-masse pour l’articulateur
est la pseudo-masse pour l’articulateur ![]() ,
,
– obtenir une trajectoire articulatoire réaliste, en minimisant  $ ; où
$ ; où  est la pseudo-constante de raideur pour l’articulateur
est la pseudo-constante de raideur pour l’articulateur ![]() . La fonction de coût à minimiser se présente donc sous la forme
. La fonction de coût à minimiser se présente donc sous la forme

|
(4.11) |
où ![]() et
et ![]() sont des constantes qui contrôlent le compromis entre la qualité acoustique et la qualité articulatoire,
sont des constantes qui contrôlent le compromis entre la qualité acoustique et la qualité articulatoire, ![]() et
et  sont les bornes de l’intervalle de temps sur lequel on conduit l’optimisation.
sont les bornes de l’intervalle de temps sur lequel on conduit l’optimisation.
L’équation 4.11 peut s’écrire sous la forme
 et le calcul variationnel [32] peut être utilisé pour minimiser
et le calcul variationnel [32] peut être utilisé pour minimiser
![]() . Le minimum de
. Le minimum de ![]() est atteint lorsque les dérivées relatives aux
est atteint lorsque les dérivées relatives aux  est nulle. Les équations d’Euler-Lagrange conduisent au système :
est nulle. Les équations d’Euler-Lagrange conduisent au système :

|
(4.12) |
Considérant la définition de ![]() , chacune des équations de ce système s’écrit :
, chacune des équations de ce système s’écrit :
 |
(4.13) |
où  est la dérivée seconde du
est la dérivée seconde du
 paramètre articulatoire par rapport au temps.
paramètre articulatoire par rapport au temps.
Considérons maintenant une unique équation de ce système par soucis de clarté ; et supposons que nous disposons d’une solution initiale grossière
 pour la trajectoire de l’articulateur
pour la trajectoire de l’articulateur ![]() entre les temps
entre les temps ![]() et
et  . Nous définissons un processus itératif tel que
. Nous définissons un processus itératif tel que
 en utilisant l’équation d’évolution :
en utilisant l’équation d’évolution :
 |
(4.14) |
où  représente l’évolution du paramètre
représente l’évolution du paramètre
 durant le processus itératif, dont la vitesse de convergence est contrôlée par
durant le processus itératif, dont la vitesse de convergence est contrôlée par ![]() . Une solution de l’équation 4.13 est obtenue quand le terme
. Une solution de l’équation 4.13 est obtenue quand le terme
 est nul. On utilise maintenant une approximation aux différences finies pour calculer les dérivées premières et secondes des paramètres articulatoires. Soit
est nul. On utilise maintenant une approximation aux différences finies pour calculer les dérivées premières et secondes des paramètres articulatoires. Soit
 la représentation discrète de la trajectoire articulatoire du paramètre
la représentation discrète de la trajectoire articulatoire du paramètre ![]() au temps
au temps
 ,
,
 la trajectoire acoustique observée et
la trajectoire acoustique observée et
 la trajectoire acoustique produite par la simulation. L’équation 4.14 ainsi discrétisée conduit à :
la trajectoire acoustique produite par la simulation. L’équation 4.14 ainsi discrétisée conduit à :
 |
(4.15) |
Le premier membre de l’équation 4.15 contient l’information acoustique tandis que le second membre représente le comportement articulatoire. Pour obtenir une unique solution au système d’équations 4.12 il nous faut des conditions aux limites. Celles-ci sont choisies de manière à ne pas fixer la position des articulateurs aux extrémités de la fenêtre temporelle, mais plutôt la régularité de la trajectoire articulatoire. On prend donc
 . L’équation 4.15 peut donc s’écrire avec ces conditions aux limites sous la forme matricielle :
. L’équation 4.15 peut donc s’écrire avec ces conditions aux limites sous la forme matricielle :

|
(4.16) |
où :
![\left\{ \begin{array}{c} B=\left[ \begin{array}{ccccc} \gamma +k_{i}\beta +m_{i}\lambda & -m_{i}\lambda & 0 & \cdots & 0\\ -m_{i}\lambda & \gamma +k_{i}\beta +2m_{i}\lambda & -m_{i}\lambda & \cdots & 0\\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & \cdots & -m_{i}\lambda & \gamma +k_{i}\beta +2m_{i}\lambda & -m_{i}\lambda \\ 0 & \cdots & 0 & -m_{i}\lambda & \gamma +k_{i}\beta +m_{i}\lambda \end{array}\right] \\ C=\left[ \begin{array}{c} \gamma \alpha _{i,0}^{\tau }-\sum ^{3}_{j=1}(f_{j,0}-F_{j,0})\frac{\partial F_{j}}{\partial \alpha }\\ \gamma \alpha _{i,1}^{\tau }-\sum ^{3}_{j=1}(f_{j,1}-F_{j,1})\frac{\partial F_{j}}{\partial \alpha }\\ \vdots \\ \gamma \alpha _{i,N}^{\tau }-\sum ^{3}_{j=1}(f_{j,N}-F_{j,N})\frac{\partial F_{j}}{\partial \alpha } \end{array}\right] \end{array}\right. \left\{ \begin{array}{c} B=\left[ \begin{array}{ccccc} \gamma +k_{i}\beta +m_{i}\lambda & -m_{i}\lambda & 0 & \cdots & 0\\ -m_{i}\lambda & \gamma +k_{i}\beta +2m_{i}\lambda & -m_{i}\lambda & \cdots & 0\\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & \cdots & -m_{i}\lambda & \gamma +k_{i}\beta +2m_{i}\lambda & -m_{i}\lambda \\ 0 & \cdots & 0 & -m_{i}\lambda & \gamma +k_{i}\beta +m_{i}\lambda \end{array}\right] \\ C=\left[ \begin{array}{c} \gamma \alpha _{i,0}^{\tau }-\sum ^{3}_{j=1}(f_{j,0}-F_{j,0})\frac{\partial F_{j}}{\partial \alpha }\\ \gamma \alpha _{i,1}^{\tau }-\sum ^{3}_{j=1}(f_{j,1}-F_{j,1})\frac{\partial F_{j}}{\partial \alpha }\\ \vdots \\ \gamma \alpha _{i,N}^{\tau }-\sum ^{3}_{j=1}(f_{j,N}-F_{j,N})\frac{\partial F_{j}}{\partial \alpha } \end{array}\right] \end{array}\right.](sites/bruno/local/cache-TeX/15ee10a98841fb6bf30f336067c07361.png?1663724204)
L’équation 4.16 conduit à un calcul itératif dans lequel on calcule  en fonction de
en fonction de
 . La solution initiale ainsi proposée à l’algorithme tend à s’améliorer dans le sens où d’une part les trajectoires articulatoires sont de plus en plus régulières et l’adéquation entre la parole prononcée et la parole de synthèse augmente. Néanmoins il n’est nullement garanti que le minimum atteint soit celui recherché, c’est pourquoi une solution initiale pour laquelle l’erreur acoustique est déjà faible tout en étant réaliste sur le plan articulatoire est intéressante. Cela justifie que nous ayons utilisé l’algorithme de Ney précédemment décrit. D’autre part, lors des expériences, nous avons fixé les pseudo-masses et pseudo-constantes de raideur à
. La solution initiale ainsi proposée à l’algorithme tend à s’améliorer dans le sens où d’une part les trajectoires articulatoires sont de plus en plus régulières et l’adéquation entre la parole prononcée et la parole de synthèse augmente. Néanmoins il n’est nullement garanti que le minimum atteint soit celui recherché, c’est pourquoi une solution initiale pour laquelle l’erreur acoustique est déjà faible tout en étant réaliste sur le plan articulatoire est intéressante. Cela justifie que nous ayons utilisé l’algorithme de Ney précédemment décrit. D’autre part, lors des expériences, nous avons fixé les pseudo-masses et pseudo-constantes de raideur à ![]() . Or ce point est améliorable puisque la mâchoire a une masse plus importante que les lèvres par exemple. Cet articulateur doit donc se mouvoir plus lentement. Par conséquent la pseudo-masse
. Or ce point est améliorable puisque la mâchoire a une masse plus importante que les lèvres par exemple. Cet articulateur doit donc se mouvoir plus lentement. Par conséquent la pseudo-masse ![]() correspondant à la mâchoire devrait être supérieure à
correspondant à la mâchoire devrait être supérieure à  qui correspond aux lèvres. Toutefois, pour ajuster ces coefficients, il aurait été intéressant d’obtenir des films articulatoires ce qui était impossible du fait des temps d’acquisition nécessaires à l’obtention d’une image IRM.
qui correspond aux lèvres. Toutefois, pour ajuster ces coefficients, il aurait été intéressant d’obtenir des films articulatoires ce qui était impossible du fait des temps d’acquisition nécessaires à l’obtention d’une image IRM.
Les trajectoires articulatoires obtenues pour les paramètres « position de la mâchoire », « position du dos de la langue » et « ouverture des lèvres » lors des expériences sur la transition /iai/ sont représentées sur la figure 4.12 tandis que la figure 4.13 illustre la précision acoustique obtenue pour cette transition. On peut noter une exagération de l’effet compensatoire entre la mâchoire et les lèvres : ceci peut s’expliquer par le fait que pour passer d’une voyelle d’arrière (/a/) à une voyelle d’avant (/i/) sans tenir compte des inerties respectives de chaque articulateur, le mouvement de la mâchoire est favorisé par rapport à celui des lèvres.
La figure 4.14 présente des trajectoires articulatoires obtenues pour les paramètres « position de la mâchoire », « position du dos de la langue » et « forme de la langue » dans le cas d’une transition /iui/. Les trajectoires des trois premiers formants correspondants sont superposées au spectrogramme de la parole prononcée par le locuteur sur la figure 4.15.
Trajectoires articulatoires pour /iai/
|
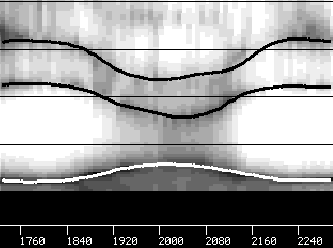
Trajectoires formantiques pour /iai/
|
Trajectoires articulatoires pour /iui/
|
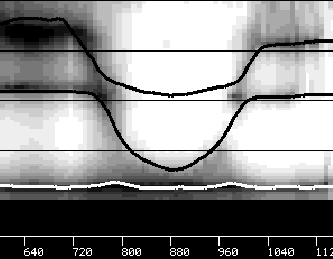
|
4.6.8 Conclusion
Notre méthode d’inversion possède l’avantage de travailler simultanément dans les domaines acoustique et articulatoire. Sans imposer de contraintes paramétriques comme, par exemple, des morceaux de trajectoires sigmoïdales, ni de position initiale et finale des articulateurs, elle conduit à des trajectoires articulatoires lisses correspondant assez fidèlement à la parole du locuteur.
Toutefois, pour pouvoir vérifier le représentativité des résultats obtenus, il nous faudrait disposer de films ce qui n’est pas encore possible avec la technologie utilisée pour l’acquisition d’images. Ceci permettrait par ailleurs de fixer les pseudo-masses ![]() et pseudo-constantes de raideur
et pseudo-constantes de raideur  de manière plus réaliste. Un autre point à développer est la recherche de valeurs optimales pour
de manière plus réaliste. Un autre point à développer est la recherche de valeurs optimales pour ![]() et
et ![]() qui contrôlent le compromis entre la qualité acoustique et la qualité articulatoire dans l’équation 4.11 de manière analogue à ce qu’ont réalisé Richards et al. [33].
qui contrôlent le compromis entre la qualité acoustique et la qualité articulatoire dans l’équation 4.11 de manière analogue à ce qu’ont réalisé Richards et al. [33].
Cependant, la méthode décrite fait preuve d’une grande flexibilité ce qui la rend adéquate pour l’étude des effets de compensation. La section suivante décrit brièvement les logiciels utilisés et ceux réalisés pour mener à bien ces expériences d’inversion acoustique-articulatoire.
4.6.9 Réalisations logicielles
Nous disposions d’une librairie de routines écrites en langage C qui implantent le modèle de Maeda4.1 : contrôle des sept paramètres et des deux facteurs d’échelle, calcul des diamètres le long du conduit vocal et passage à la fonction d’aire à l’aide des coefficients de Heinz et Stevens, simulation fréquentielle, simulation temporelle utilisant un modèle de la source glottale. Nous avions aussi à notre disposition le logiciel Snorri (cf. figure 4.16) qui est un outil d’analyse de la parole et permet en particulier d’extraire les formants en implantant différents algorithmes d’analyse de la parole.
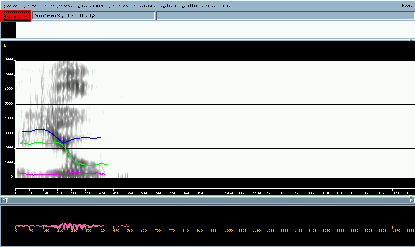
Snorri
|
Fenêtre principale Maeda
|
Sur cette base, nous avons réalisé une classe en C++ qui encapsule les routines C. Une interface graphique a aussi été développée. L’utilisateur dispose alors d’une boite de dialogue pour changer les valeurs des constantes physiques utilisées lors de la simulation (densité de l’air, pressions...), une autre pour contrôler les paramètres articulatoires du modèle et modifier les facteurs d’échelle respectifs de la bouche et du pharynx. La fenêtre principale affiche la fonction d’aire (figure 4.17). Elle comporte une barre de menus à partir de laquelle il est possible d’accéder aux boites de dialogues et de synthétiser puis d’écouter la voyelle correspondant aux paramètres articulatoires. Depuis ces menus, il est encore possible de donner un triplet de formants à atteindre à partir de la configuration articulatoire courante, soit en « optimisant » la paroi dure, soit en recherchant des paramètres articulatoires proches de la position initiale. Le calcul des fonctions de sensibilité (cf. [34]) et leur affichage ( en fonction de
en fonction de  ) est aussi disponible. La fonction d’aire est synchronisée avec la coupe sagittale mais l’utilisateur peut aussi la modifier interactivement. Les valeurs des formants (qui sont synchronisées avec la fonction d’aire) sont affichées avec le spectre de transfert et la coupe sagittale du conduit dans une autre fenêtre (figure 4.18). Enfin, les résultats de l’inversion peuvent être récupérés pour animer la coupe sagittale.
) est aussi disponible. La fonction d’aire est synchronisée avec la coupe sagittale mais l’utilisateur peut aussi la modifier interactivement. Les valeurs des formants (qui sont synchronisées avec la fonction d’aire) sont affichées avec le spectre de transfert et la coupe sagittale du conduit dans une autre fenêtre (figure 4.18). Enfin, les résultats de l’inversion peuvent être récupérés pour animer la coupe sagittale.

Coupe sagittale, spectre et formants
|
Un autre programme a été développé pour extraire manuellement les contours du conduit vocal à partir des images IRM du conduit vocal, projeter les contours ainsi obtenus sur la grille semi-polaire puis calculer les paramètres articulatoires du modèle de Maeda qui produisent le contour le plus proche.
Le filtrage non-linéaire de Ney a été implanté par un programme qui prend en entrée un dictionnaire et une trajectoire acoustique. Il est paramétré par la valeur du bonus (cf. section 4.6.7). Il fournit le fichier initial utilisé par le programme de calcul variationnel.
L’optimisation a été implantée sous la forme d’un autre programme qui prend en entrée un fichier contenant la trajectoire initiale, c’est-à-dire pour chaque pas de temps, d’une part un ensemble de paramètres articulatoires initialement filtré par l’algorithme de Ney, et d’autre part les trois formants extraits de la parole du locuteur. Elle fournit un nouveau fichier à chaque pas d’itération, dans lequel les paramètres articulatoires ont évolué. Ce fichier peut être utilisé pour animer le modèle dans l’interface graphique.
Notes
[1] S. Maeda.
Une analyse statistique sur les positions de la langue : Etude
préliminaire sur les voyelles françaises.
In IXèmes Journées d’Etude sur la Parole, pages 191-199,
Lannion, France, June 1978.
[2] S. Maeda.
Un modèle de la langue avec des composantes linéaires.
In Xèmes Journées d’Etude sur la Parole, pages 152-162,
Lannion, France, May 1979.
[3] J.E. Overall.
Orthogonal factors and uncorrelated factor scores.
In Psychological Reports, volume 10, pages 651-662, 1962.
[4] M. Stone, M.H. Goldstein Jr., and Y. Zhang.
Principal component analysis of cross sections of tongue shapes in
vowel production.
In 1st ESCA Tutorial and Research Workshop on Speech
Production Modeling : From Control Strategies to Acoustics Speech
Production Seminar : Models and Data, pages 37-40, Autrans, France, 1996.
[5] G. Fant.
Vocal-tract area and length perturbations.
STL-QPSR, pages 1-14, January 1975.
[6] U. G. Goldstein.
An Articulatory Model for the Vocal Tracts of Growing Children.
PhD thesis, Massachusetts Institute of Technology, June 1980.
[7] B. Mathieu and Y. Laprie.
Speaker normalization of the Maeda’s model.
In Proceeding of International Workshop on Speech and Computer,
SPECOM’96, pages 167-170, St. Petersburg, Russia, October 1996.
[8] B. Mathieu and Y. Laprie.
Adaptation of Maeda’s model for acoustic to articulatory inversion.
In Proceedings of the 5th European Conference on Speech
Communication and Technology, volume 4, pages 2015-2018, Rhodes, Greece,
September, 1997.
[9] C.-S. Yang and H. Kasuya.
Accurate measurement of vocal tract shapes from magnetic resonance
images of child, female and male subjects.
In ICSLP, pages 623-626, Yokohama, Japan, September 1994.
[10] S. Maeda and R. Carré.
Modèles de production.
In Fondements et perspectives en reconnaissance automatique de
la parole, pages 51-72, 1995.
[11] W. J. Strong and E. P. Palmer.
Formant estimation from linear prediction spectra and their second
derivatives.
In J. Acoust. Soc. Am., volume 55, page 396, 1974.
[12] A. Soquet.
Etude comparée de représentations acoustiques et articulatoires
du signal de parole pour le décodage acoustico-phonétique.
PhD thesis, Univ. Libre de Bruxelles, 1995.
[13] U. G. Goldstein.
An Articulatory Model for the Vocal Tracts of Growing Children.
PhD thesis, Massachusetts Institute of Technology, June 1980.
[14] G. Fant.
Vocal-tract area and length perturbations.
STL-QPSR, pages 1-14, January 1975.
[15] W.H. Press, S.A. Teukolsky, W.T. Vetterling, and B.P. Flannery.
Numerical Recipes in C, The Art of Scientific Computing.
Cambridge University Press, 1992.
[16] L. Candille and H. Méloni.
Automatic speech recognition using procuction models.
In ICPhS 95, volume 4, pages 256-259, 1995.
[17] B. H. Story, I. R. Tize, and E. A. Hoffman.
Vocal tract area functions from magnetic resonance imaging.
Journal of Acoustical Society of America, 100(1):537-553, July
1996.
[18] J. M. Heinz and K. N. Stevens.
On the relations between lateral cineradiographs, area functions and
acoustic spectra of speech.
In 5th International Congress on Acoustics, A44, Liège, 1965.
[19] V. Lecuit.
Sagittal cut to area function transformation : a comparative
study.
PhD thesis, Mémoire de licence en sciences physiques, Univ. Libre de
Bruxelle, 1995.
[20] D. Beautemps, P. Badin, G. Bailly, A. Galvan, and R. Laboissière.
Evaluation of an articulatory-acoustic model based on a reference
subject.
In 1st ESCA Tutorial and Research Workshop on Speech Production
Modeling., pages 45-48, Autrans, France, 1996.
[21] Y. Laprie and M.-O. Berger.
Cooperation of regularization and speech heuristics to control
automatic formant tracking.
Speech Communication, 19(4):255-270, October 1996.
[22] L. Candille.
Modèles de Production et Reconnaissance Automatique de la
Parole.
PhD thesis, Univ. d’Avignon et des Pays de Vaucluse, 1996.
[23] M. George.
Analyse du signal de parole par modélisation de la cinématique
de la fonction d’aire du conduit vocal.
PhD thesis, Univ. Libre de Bruxelles, 1997.
[24] L.-J. Boë, P. Perrier, and G. Bailly.
The geometric vocal tract variables controlled for vowel production :
proposals for constraining acoustic-to-articulatory inversion.
Journal of Phonetics, 20:27-38, 1992.
[25] L. Candille and H. Méloni.
Automatic speech recognition using procuction models.
In ICPhS 95, volume 4, pages 256-259, 1995.
[26] D. Beautemps and B. Gabioud.
Adaptation d’un modèle articulatoire à un locuteur dans le but de
contraindre l’inversion articulatori-acoustique.
In XXèmes Journées d’Etude sur la Parole, pages 119-124,
Trégastel, France, June 1994.
[27] H. Ney.
A dynamic programmation algorithm for nonlinear smoothing.
Signal Processing, 5(2):163-173, March 1983.
[28] Y. Laprie and B. Mathieu.
Inversion acoustique articulatoire par une méthode
variationnelle.
In Actes des 22èmes Journées d’Etude sur la Parole,
pages 295-298, Martigny, Switzerland, June 1998.
[29] Y. Laprie and B. Mathieu.
Inversion acoustique articulatoire par une méthode
variationnelle.
In Actes des 22èmes Journées d’Etude sur la Parole,
pages 295-298, Martigny, Switzerland, June 1998.
[30] S. Maeda.
Articulatory co-ordination and its neurobiological aspects : an essay.
In ICPhS, volume 2, pages 76-83, Stockholm, August 1995.
[31] Y. Laprie and B. Mathieu.
Inversion acoustique articulatoire par une méthode
variationnelle.
In Actes des 22èmes Journées d’Etude sur la Parole,
pages 295-298, Martigny, Switzerland, June 1998.
[32] R.S. Schechter.
The variational Method in Engineering.
McGraw-Hill Book Comp., New York, 1967.
[33] H. B. Richards, J. S. Bridle, M. J. Hunt, and J. S. Mason.
Dynamic constraint weighting in the context of articulatory parameter
estimation.
In Proceedings of the 5th European Conference on Speech
Communication and Technology, pages 2535-2538, Rhodes, Greece, September,
1997.
[34] L.-J. Boë, P. Badin, and P. Perrier.
Fron sensitivity functions......to macro-variations.
In ICPhS, volume 2, pages 234-237, Stockholm, August 1995.
 (%)
(%)

