Résumé–Sommaire

4.2 La production de la parole

Dans « Speaking : from intention to articulation » Levelt [1] explique comment l’homme exprime ses intentions au moyen de la parole. La première étape constitue ce que l’auteur appelle la conceptualisation : le locuteur utilise les connaissances qu’il a de lui et du monde (dans sa mémoire à long terme) ainsi que des connaissances sur le discours qu’il conduit (dans sa mémoire à court terme) pour produire un message préverbal. Celui-ci est ensuite encodé à l’aide de la grammaire du langage du locuteur en accédant au lexique pour produire la structure de surface. Puis un plan phonétique ou plan articulatoire est construit grâce à l’encodage phonologique. Vient alors l’articulation, qui consiste à exécuter le plan articulatoire c’est-à-dire à déplacer les muscles qui contrôlent le flux d’air à l’intérieur du conduit vocal, ce qui s’accompagne de l’émission du signal sonore.

Cependant, dans cette partie nous nous intéresserons uniquement aux aspects articulatoires et acoustiques de la production. N’oublions pas en effet que notre but est de reconnaître la parole, en tenant compte des contraintes articulatoires inhérentes à l’anatomie du conduit vocal et ainsi de tenter de modéliser dans une certaine mesure la variabilité du signal acoustique due à la coarticulation. Pour remonter aux intentions du locuteur, il faut comprendre les phrases prononcées ce qui nécessite de résoudre des problèmes liés à la référence, l’accès au lexique... qui sont d’autres vastes domaines de recherche.

4.2.1 Le conduit vocal

Une coupe sagittale de conduit vocal est représentée sur la figure 4.1.

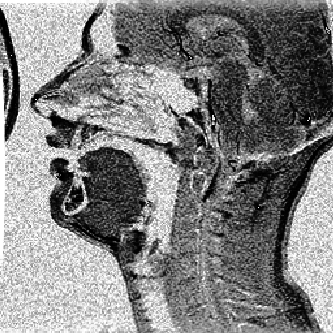
**Figure 4.1 :** Coupe sagittale du conduit vocal (voyelle /i/)
Coupe sagittale du conduit vocal (voyelle /i/)

Bien que le conduit vocal soit tridimensionnel, la coupe sagittale donne une bonne description de la plupart des phonèmes. En outre l’acquisition de données anatomiques non invasive n’est pas encore chose aisée. Et les données les plus nombreuses sont encore les radiographies de conduits vocaux et par conséquent des vues bidimensionnelles [2]. Cependant on peut fonder de grands espoirs sur l’imagerie par résonance magnétique (IRM) [3]. En effet, si cette technique—qui permet de découper le conduit vocal selon n’importe quel plan—nécessite encore une longue exposition pour collecter une image, ces durées diminuent. Par ailleurs, la qualité de l’image ainsi obtenue est incomparable à la médiocrité des clichés radiographiques.

La parole est produite par l’air qui, expulsé des poumons via la trachée, traverse la cavité pharyngale puis les cavités orales et/ou nasales. Pour les sons voisés, la glotte vibre. Les sons fricatifs sont dûs à un rétrécissement du conduit qui génère des bruits de friction. Les occlusives sont caractérisées par une fermeture totale du conduit durant un bref instant. Les nasales sont produites par l’abaissement du vélum.

Par ailleurs, il semble que les configurations articulatoires dans le plan sagittal soient assez invariantes pour produire certains sons. Si les voyelles standard peuvent être décrites dans l’espace acoustique F1-F2, elles peuvent l’être aussi en fonction du degré d’ouverture (bien qu’il ne soit pas aisé à définir [4]) et de la position de la principale constriction du conduit. En outre, les occlusives aussi sont bien caractérisées par la position de sa fermeture.

Nous présenterons seulement le modèle du conduit vocal. Un modèle de production complet doit aussi intégrer les sources. Il en va ainsi dans l’optique de faire de la synthèse ou du codage articulatoire [5]. Or dans le cas de la reconnaissance de parole (au sens speech to text) nous pensons que l’encodage du texte est principalement contrôlé par la forme du conduit vocal, tandis que les sources (le contrôle de la glotte plus précisément) encodent plutôt des informations relatives au locuteur comme son identité et son état émotionnel par exemple.

4.2.2 Les équations acoustiques

Dans cette partie les quantités suivantes : distribution de vitesse volumique
$\bf v$ , pression , densité $\rho$ dépendent des 3 variables spatiales et du temps sauf indication contraire.

4.2.2.1 Équations de Navier-Stockes et d’Euler

L’écoulement de l’air dans le conduit vocal est régit par les équations de Navier-Stockes [6]

$\rho [\frac{\partial {\bf v}}{\partial t}+({\bf v\nabla }){\bf v}]=-{\bf grad}\, p+\eta \triangle {\bf v}+(\zeta +\frac{\eta }{3}){\bf grad}\, {\rm div}\, {\bf v}$

(4.1)

où $\rho$ est la densité du fluide, $\zeta$ et $\eta$ leurs coefficients de viscosité (qui sont supposés ne pas dépendre de la température ni de la pression du fluide), $\bf v$ est sa vitesse volumique et sa pression.

Or résoudre cette équation n’est pas une mince affaire, c’est pourquoi des approximations sont faites. Dans un premier temps on peut considérer que l’on a affaire à un fluide parfait ce qui annule $\zeta$ et $\eta$ . Les équations obtenues :

$\frac{\partial {\bf v}}{\partial t}+({\bf v\nabla }){\bf v}=-\frac{{\bf grad}\, p}{\rho }$

(4.2)

sont encore appelées équations d’Euler, ou équations de conservation de mouvement.

Ensuite, la vitesse volumique est faible et on peut négliger le terme
$({\bf v\nabla }){\bf v}$ dans ces équations. D’autre part, si la vitesse volumique est faible, alors les variations de pression et de densité sont petites elles aussi. Soit la variation de la pression autour de la pression de référence $p_{0}$ et $\rho ’,\, \rho _{0}$ les grandeurs équivalentes pour la densité, les équations d’Euler se réduisent alors à :

$\frac{\partial {\bf v}}{\partial t}+\frac{{\bf grad}\, p’}{\rho _{0}}=0$

(4.3)

où $p’=p-p_{o}$ et $\rho _{0}=\rho -\rho ’$ .

4.2.2.2 Équation de continuité

Cette équation traduit le fait que la matière se conserve. Soit un volume $V_{o}$ d’air de masse $\int _{V_{0}}\rho dV$ , la masse d’air qui sort de ce volume par unité de temps vaut $\oint _{V_{0}}\rho {\bf vdf}$ où $\bf df$ est un vecteur normal à la surface du volume $V_{o}$ orienté vers l’extérieur de $V_{o}$ dont la norme égale l’aire de l’élément de surface. Or la masse d’air sortant du volume vaut aussi
$-\frac{\partial }{\partial t}\int _{V_{0}}\rho dV$ par unité de temps. On a donc

$\frac{\partial }{\partial t}\int _{V_{0}}\rho dV=-\oint _{V_{0}}\rho {\bf vdf}$ .

En transformant l’intégrale de surface en intégrale de volume on obtient

$\frac{\partial }{\partial t}\int _{V_{0}}\rho dV=-\int _{V_{0}}{\rm div}\, \rho {\bf vdf}$ .

Or cette équation doit être vérifiée pour tout volume , il faut donc que les quantités sous le signe d’intégration soient nulles. Ceci conduit à l’équation de continuité, aussi appelée équation de conservation de masse :

$\frac{\partial \rho }{\partial t}+{\rm div}\, \rho {\bf v}=0$

(4.4)

En utilisant les approximations faites sur $v,\rho$ et nous obtenons l’équation de continuité :

$\partial \rho ’}{\partial t}+\rho _{0}{\rm div}\, {\bf v}=0 \end{equation}$

(4.5)

4.2.2.3 Équation d’état du fluide parfait

Arrivés à ce stade, nous avons 3 équations d’Euler et une équation de continuité pour 5 inconnues : les 3 composantes du vecteur vitesse, la variation de pression et la variation de densité. Il nous faut donc une dernière équation pour résoudre le problème. Dans un fluide parfait le mouvement est un processus adiabatique, ce qui permet de lier $\rho ’$ et :

$p’=\left( \frac{\partial p}{\partial \rho }\right) _{s}\rho ’$

(4.6)

où est l’entropie du fluide.

4.2.2.4 Équation d’onde

Maintenant posons

${\bf v}={\bf grad}\, \varphi$

(4.7)

$\varphi$ étant le potentiel des vitesses. On déduit alors des équations d’Euler

$-\frac{p’}{\rho _{o}}=\frac{\partial \varphi }{\partial t}$

(4.8)

puis l’équation de continuité conduit à l’équation d’onde

$\frac{\partial ^{2}\varphi }{\partial t^{2}}-c^{2}\triangle \varphi =0$

(4.9)

en posant
$c=\sqrt{\left( \frac{\partial p}{\partial \rho }\right) _{s}}$ (célérité du son).

L’équation 4.9, vérifiée par le potentiel des vitesses, l’est aussi pour chaque composante de la distribution de vitesse (appliquer à l’équation 4.7 l’opérateur ${\bf grad}$ ) ainsi que pour (appliquer à l’équation 4.8 l’opérateur
$\frac{\partial }{\partial t}$ ) et par conséquent pour $\rho ’$ (d’après l’équation 4.6).

4.2.2.5 Équation de Webster

Jusqu’à présent, nous avons fait des hypothèses sur le flux d’air. Il faut maintenant préciser la géométrie du conduit vocal. Il est souvent modélisé par un tube droit de section circulaire $A(x,t)$ . Souvent on considère le tube statique à parois rigides : ne dépend que de qui varie de la glotte aux lèvres. La vitesse à l’intérieur du tube vaut alors $v=\frac{u}{A}$ où est le débit dans le conduit. Dans ce cas, les équations d’Euler et de continuité mènent à :

$\frac{\rho _{0}}{A}\frac{\partial u}{\partial t}+\frac{\partial p’}{\partial x}=0$

$\frac{\partial p’}{\partial t}+\rho _{0}c^{2}\frac{\partial }{\partial x}\frac{u}{A}=0$

En dérivant la seconde équation par rapport au temps nous dérivons la célèbre équation de Webster :

$\frac{1}{A}\frac{\partial }{\partial x}\left[ A\frac{\partial p’}{\partial x}\right] +\frac{1}{c^{2}}\frac{\partial ^{2}p’}{\partial t^{2}}=0$

(4.10)

4.2.2.6 Conduit nasal et cavité sous-glottique

Pour modéliser le conduit nasal, il suffit de considérer 3 tubes. Le premier correspond au pharynx, les deux autres respectivement à la bouche et au conduit nasal. Les conditions à la jonction du pharynx et des deux autres tubes permettent de résoudre l’équation 4.10.

On peut de la même manière prendre en compte la cavité sous-glottique qui introduit des zéros dans le spectre de parole. Cependant, lorsque la glotte est fermée, le couplage entre les cavités sous et supra-glottique est faible et il est possible de négliger la partie inférieure du conduit.

4.2.2.7 Les sources

Lorsque l’on veut simuler la production de la parole, il faut aussi prendre en compte les sources. Celles-ci sont :

–

[7]

–

4.2.3 Méthodes de résolution

4.2.3.1 Modèles du conduit vocal

Différents choix peuvent être faits pour la fonction d’aire . Si l’on considère le tube uniforme (ou une concaténation de tubes uniformes), l’analogie électrique permet d’effectuer les simulations. Celles-ci peuvent s’effectuer dans le domaine temporel, dans le domaine fréquentiel ou encore dans les deux à la fois (en modélisant les sources dans le domaine temporel et le conduit dans le domaine fréquentiel [8]).

Toutefois, quand on s’intéresse plus particulièrement aux modes de résonance du conduit, il n’est pas toujours nécessaire de résoudre l’équation de Webster en calculant le spectre de transfert du conduit vocal.

Si l’on développe en série de Fourier la fonction d’aire [9] ou son logarithme [10], la théorie des perturbations offre un cadre efficace pour calculer les fréquences propres de l’équation de Webster.

Plus généralement, le calcul variationnel [11] n’impose pas de contraintes à la fonction d’aire et fournit une manière efficace pour calculer les fréquences des formants.

Nous allons présenter la simulation par analogie électrique dans le domaine fréquentiel car les formants (fréquences, largeurs de bande et amplitudes) peuvent être calculés efficacement à partir du spectre produit.

4.2.3.2 Analogie électrique

Représentons le conduit vocal par une concaténation de tubes uniformes. En cherchant les solutions de l’équation d’onde sous la forme d’ondes monochromatiques
$\phi (x,t)=\psi (x)e^{j\omega t}$ , nous obtenons pour chaque tube :

$\frac{\partial ^{2}\psi }{\partial x^{2}}+\frac{\omega ^{2}}{c^{2}}\psi =0$

**Figure 4.2 :** Elément de circuit électrique
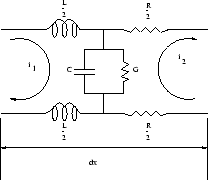
Elément de circuit électrique

Maintenant, en posant $y=G+j\omega C$ et $z=R+j\omega L$ et en considérant les 2 branches dans lesquelles circulent respectivement les courant $i_{1}$ et $i_{2}$ , les équations suivantes sont vérifiées pour la ligne de transmission représentée sur la figure 4.2 :

$\left\{ \begin{array}{c} {\,\rm d}I=-Ey{\,\rm d}x\\ {\,\rm d}E=-Iz{\,\rm d}x \end{array}\right.$

d’où le système :

$\left\{ \begin{array}{c} \frac{{\,\rm d}^{2}E}{{\,\rm d}x^{2}}-yzE=0\\ \frac{{\,\rm d}^{2}I}{{\,\rm d}x^{2}}-yzI=0 \end{array}\right.$

en posant $\gamma ^{2} = yz = -\frac{\omega ^{2}}{c^{2}}=$
( $\gamma$ est appelé constante de propagation) nous constatons que ces équations sont analogues à l’équation d’onde, la pression correspondant à la tension et le débit au courant . Dans le cas où il n’y a pas de pertes, $\gamma =\pm j\frac{\omega }{c}=\pm j\omega \sqrt{LC}$ est imaginaire pur. Les composants résistifs et permettent de tenir compte des pertes thermiques et de celles dues à la viscosité de l’air. Les solutions sont :

$E=A_{1}e^{\gamma x}+B_{1}e^{-\gamma x}$

$I=A_{2}e^{\gamma x}+B_{2}e^{-\gamma x}$

où
$A_{1},\, A_{2},\, B_{1}$ et $B_{2}$ sont des constantes déterminées par les conditions initiales. En considérant une section de longueur de la ligne de transmission, dont les différences de potentiel sont $E_{1}$ en entrée et $E_{2}$ à la sortie, et parcourue par les courants $I_{1}$ et $I_{2}$ nous obtenons :

$\left\{ \begin{array}{c} E_{1}=\sqrt{\frac{z}{y}}I_{1}\coth \gamma l+\sqrt{\frac{z}{y}}I_{2}\csc \gamma l\\ E_{2}=\sqrt{\frac{z}{y}}I_{1}\csc \gamma l+\sqrt{\frac{z}{y}}I_{2}\coth \gamma l \end{array}\right.$

Ce système relie les tensions (équivalent électrique de la pression acoustique) aux courants (équivalent de la vitesse volumique) observés aux bornes du quadripôle (équivalent d’un élément de conduit vocal) sous forme simple. En concaténant de simples tubes, on obtient alors un modèle du conduit vocal. Pour les voyelles, les pressions et les vitesses peuvent ainsi être calculées de proche en proche le long du conduit lorsque l’on dispose d’un modèle de la glotte.

4.2.4 Conclusion

À partir des équations d’Euler (équations 4.2 ), de continuité (équation 4.5) et d’état (équation 4.6), différentes dérivations ajoutées aux hypothèses sur la fonction d’aire permettent de calculer les fréquences des modes de résonance du conduit vocal sans forcément passer par le calcul de la fonction de transfert. Les approximations faites lors de la dérivation des équations n’influent pas beaucoup sur les fréquences des formants. Comme l’inversion acoustique-articulatoire est souvent basée sur les formants extraits du signal acoustique, toutes ces méthodes peuvent être utilisées en première approximation pour résoudre ce problème. Cependant pour faire de la synthèse de parole il faut prendre en compte les sources ainsi que les pertes qui sont primordiales dans l’évaluation des largeurs de bandes associées aux formants afin d’obtenir un timbre naturel. Ceci peut être accompli en faisant d’autres approximations (voir par exemple [12]) ou en introduisant des impédances pour chacune des pertes dans l’analogie électrique [13]. La section suivante présente différents modèles ayant pour but de contrôler l’aire du conduit avec peu de paramètres.

Notes

[1] W.J.M. Levelt.

Speaking : From intention to articulation.

MIT Press, 1989.

[2] A. Bothorel.

Cinéradiographie des voyelles et consonnes du français.

Publications de l’Institut de Phonétique de Strasbourg, 1986.

[3] F.-R. Verdun and A.G. Marshall.

Transformée de Fourier Applications en RMN et IRM.

Masson, 1995.

[4] M. Rossi.

Niveaux de l’analyse phonétique : nature et structuration des indices
et des traits.

Speech Communication, 2:91-106, 1983.

[5] M.M. Sondhi and J. Schroeter.

A hybrid time-frequency domain articulatory speech synthesizer.

IEEE Trans. on Acoust., Speech and Signal Processing,
35(7):955-967, July 1987.

[6] L. Landau and E. Lifchitz.

Mécanique des fluides, chapter 2, page 69.

Librairie du globe, 1989.

[7] K. Ishizaka and J. L. Flanagan.

Acoustic properties of a two-mass model of the vocal cords.

Bell Syst. Technol. J., 51:1233-1268, 1972.

[8] M.M. Sondhi and J. Schroeter.

A hybrid time-frequency domain articulatory speech synthesizer.

IEEE Trans. on Acoust., Speech and Signal Processing,
35(7):955-967, July 1987.

[9] Z. Yu.

A method to determine the area function of speech based on
perturbation therory.

STL-QPSR, 4:77-94, 1993.

[10] H. Yehia and F. Itakura.

A method to combine acoustic and morphological constrints in the
production inverse problem.

Speech Communication, 18:151-174, 1996.

[11] P. Jospa.

Formulation variationnelle du lien acoustico-articulatoire.

In XXèmes Journées d’Etude sur la Parole, pages 113-118,
Trégastel, France, June 1994.

[12] M. M. Sondhi.

Model for wave propagation in a lossy vocal tract.

J. Acoust. Soc. Amer., 55(5):1070-1075, May 1974.
],[M. Mrayati and B. Guerin.

Étude des caractéristiques acoustiques des voyelles orales françaises
par simulation du conduit vocal avec pertes.

Revue d’Acoustique, 36:18-32, 1976.

[13] J. L. Flanagan.

Speech Analysis Synthesis and Perception.

Springer-Verlag, New-York, 1972.